Information to lightning-fast JAX

Hey there, fellow Python fanatic! Have you ever ever wished your NumPy code run at supersonic pace? Meet JAX!. Your new finest buddy in your machine studying, deep studying, and numerical computing journey. Consider it as NumPy with superpowers. It will possibly mechanically deal with gradients, compile your code to run quick utilizing JIT, and even run on GPU and TPU with out breaking a sweat. Whether or not you’re constructing neural networks, crunching scientific knowledge, tweaking transformer fashions, or simply making an attempt to hurry up your calculations, JAX has your again. Let’s dive in and see what makes JAX so particular.

This information offers an in depth introduction to JAX and its ecosystem.

Studying Aims

• Clarify JAX’s core ideas and the way they differ from Numpy.
• Apply JAX’s three key transformations to optimize Python code. Convert NumPy operations into environment friendly JAX implementation.
• Determine and repair frequent efficiency bottlenecks in JAX code. Implement JIT compilation accurately whereas avoiding typical Pitfalls.
• Construct and practice a Neural Community from scratch utilizing JAX. Implement frequent machine studying operations utilizing JAX’s practical strategy.
• Resolve optimization issues utilizing JAX’s computerized differentiation. Carry out environment friendly matrix operations and numerical computations.
• Apply efficient debugging methods for JAX-specific points. Implement memory-efficient patterns for large-scale computations.

This text was printed as part of the Knowledge Science Blogathon.

What’s JAX?

In keeping with the official documentation, JAX is a Python library for acceleration-oriented array computation and program transformation, designed for high-performance numerical computing and large-scale machine studying. So, JAX is basically NumPy on steroids, It combines acquainted NumPy-style operations with computerized differentiation and {hardware} acceleration. Consider it as getting the most effective of three worlds.

• NumPy’s elegant syntax and array operation
• PyTorch like computerized differentiation functionality
• XLA’s (Accelerated Linear Algebra) for {hardware} acceleration and compilation advantages.

Why does JAX Stand Out?

What units JAX aside is its transformations. These are highly effective capabilities that may modify your Python code:

• JIT: Simply-In-Time compilation for sooner execution
• Grad: Automated differentiation for computing gradients
• vmap: Routinely vectorization for batch processing

Here’s a fast look:

import jax.numpy as jnp
from jax import grad, jit
# Outline a easy perform
@jit  # Velocity it up with compilation
def square_sum(x):
    return jnp.sum(jnp.sq.(x))
# Get its gradient perform mechanically
gradient_fn = grad(square_sum)
# Attempt it out
x = jnp.array([1.0, 2.0, 3.0])
print(f"Gradient: {gradient_fn(x)}")

Output:

Gradient: [2. 4. 6.]

Getting Began with JAX

Beneath we are going to comply with some steps to get began with JAX.

Step1: Set up

Establishing JAX is easy for CPU-only use. You need to use the JAX documentation for extra info.

Step2: Creating Atmosphere for Mission

Create a conda atmosphere in your challenge

# Create a conda env for jax
$ conda create --name jaxdev python=3.11

#activate the env
$ conda activate jaxdev

# create a challenge dir title jax101
$ mkdir jax101

# Go into the dir
$cd jax101

Step3: Putting in JAX

Putting in JAX within the newly created atmosphere

# For CPU solely
pip set up --upgrade pip
pip set up --upgrade "jax"

# for GPU
pip set up --upgrade pip
pip set up --upgrade "jax[cuda12]"

Now you’re able to dive into actual issues. Earlier than getting your arms soiled on sensible coding let’s be taught some new ideas. I will likely be explaining the ideas first after which we are going to code collectively to grasp the sensible viewpoint.

First, get some motivation, By the best way, why will we be taught a brand new library once more? I’ll reply that query all through this information in a step-by-step method so simple as potential. 

Why Be taught JAX?

Consider JAX as an influence instrument. Whereas NumPy is sort of a dependable hand noticed, JAX is sort of a fashionable electrical noticed. It requires a bit extra steps and data, however the efficiency advantages are price it for intensive computation duties.

• Efficiency: Jax code can run considerably sooner than Pure Python or NumPy code, particularly on GPU and TPUs
• Flexibility: It’s not only for machine learning- JAX excels in scientific computing, optimization, and simulation.
• Trendy Method: JAX encourages practical programming patterns that result in cleaner, extra maintainable code.

Within the subsequent part, we’ll dive deep into JAX’s transformation, beginning with the JIT compilation. These transformations are what give JAX its superpowers, and understanding them is vital to leveraging JAX successfully.

Important JAX Transformations

JAX’s transformations are what really set it other than the numerical computation libraries comparable to NumPy or SciPy. Let’s discover every one and see how they will supercharge your code.

JIT or Simply-In-Time Compilation

Simply-in-time compilation optimizes code execution by compiling components of a program at runtime reasonably than forward of time.

How JIT works in JAX?

In JAX, jax.jit transforms a Python perform right into a JIT-compiled model. Adorning a perform with @jax.jit captures its execution graph, optimizes it, and compiles it utilizing XLA. The compiled model then executes, delivering vital speedups, particularly for repeated perform calls.

Right here is how one can strive it.

import jax.numpy as jnp
from jax import jit
import time


# A computationally intensive perform
def slow_function(x):
    for _ in vary(1000):
        x = jnp.sin(x) + jnp.cos(x)
    return x


# The identical perform with JIT
@jit
def fast_function(x):
    for _ in vary(1000):
        x = jnp.sin(x) + jnp.cos(x)
    return x

Right here is similar perform, one is only a plain Python compilation course of and the opposite one is used as a JAX’s JIT compilation course of. It’ll calculate the 1000 knowledge factors sum of sine and cosine capabilities. we are going to examine the efficiency utilizing time.

# Examine efficiency
x = jnp.arange(1000)

# Heat-up JIT
fast_function(x)  # First name compiles the perform

# Time comparability
begin = time.time()
slow_result = slow_function(x)
print(f"With out JIT: {time.time() - begin:.4f} seconds")

begin = time.time()
fast_result = fast_function(x)
print(f"With JIT: {time.time() - begin:.4f} seconds")

The outcome will astonish you. The JIT compilation is 333 occasions sooner than the traditional compilation. It’s like evaluating a bicycle with a Buggati Chiron.

Output:

With out JIT: 0.0330 seconds
With JIT: 0.0010 seconds

JIT may give you a superfast execution increase however you could use it correctly in any other case it is going to be like driving Bugatti on a muddy village highway that provides no supercar facility.

Widespread JIT Pitfalls

JIT works finest with static shapes and kinds. Keep away from utilizing Python loops and situations that rely upon array values. JIT doesn’t work with the dynamic arrays.

# Dangerous - makes use of Python management move
@jit
def bad_function(x):
    if x[0] > 0:  # This may not work nicely with JIT
        return x
    return -x


# print(bad_function(jnp.array([1, 2, 3])))


# Good - makes use of JAX management move
@jit
def good_function(x):
    return jnp.the place(x[0] > 0, x, -x)  # JAX-native situation


print(good_function(jnp.array([1, 2, 3])))

Output:

Which means bad_function is dangerous as a result of JIT was not positioned within the worth of x throughout calculation.

Output:

[1 2 3]

Limitations and Issues

• Compilation Overhead: The primary time a JIT-compiled perform is executed, there’s some overhead because of compilation. The compilation price could outweigh the efficiency advantages for small capabilities or these referred to as solely as soon as.
• Dynamic Python Options: JAX’s JIT requires capabilities to be “static”. Dynamic management move, like altering shapes or values based mostly on Python loops, is just not supported within the compiled code. JAX supplied alternate options like `jax.lax.cond` and `jax.lax.scan` to deal with dynamic management move.

Automated Differentiation

Automated differentiation, or autodiff, is a computation method for calculating the spinoff of capabilities precisely and successfully. It performs a vital function in optimizing machine studying fashions, particularly in coaching neural networks, the place gradients are used to replace mannequin parameters.

How does Automated differentiation work in JAX?

Autodiff works by making use of the chain rule of calculus to decompose advanced capabilities into less complicated ones, calculating the spinoff of those sub-functions, after which combining the outcomes. It information every operation through the perform execution to assemble a computational graph, which is then used to compute derivatives mechanically.

There are two fundamental modes of auto-diff:

• Ahead Mode: Computes derivatives in a single ahead cross by means of the computational graph, environment friendly for capabilities with a small variety of parameters.
• Reverse Mode: Computes derivatives in a single backward cross by means of the computational graph, environment friendly for capabilities with a lot of parameters.

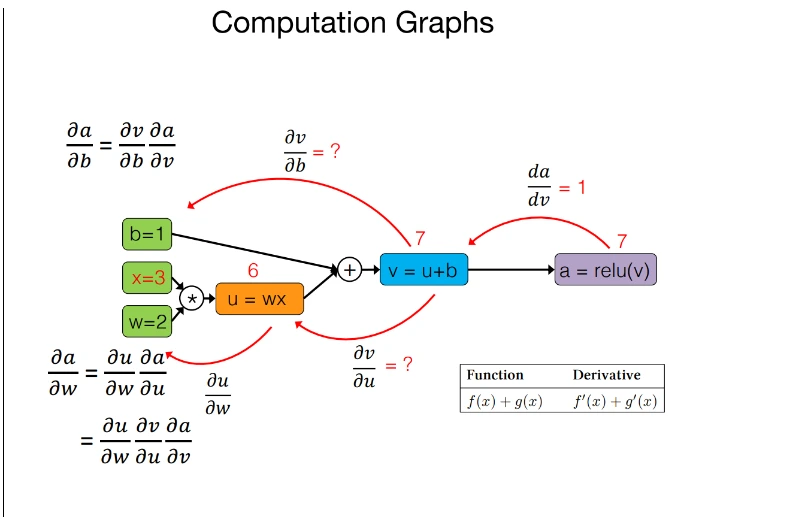
Key options in JAX computerized differentiation

• Gradient Computation(jax.grad): `jax.grad` computes the spinoff of a scaler-output perform for its enter. For capabilities with a number of inputs, a partial spinoff may be obtained.
• Greater-Order Spinoff(jax.jacobian, jax.hessian) :   JAX helps the computation of higher-order derivatives, comparable to Jacobians and Hessains, making it appropriate for superior optimization and physics simulation.
• Composability with different JAX Transformation:   Autodiff in JAX integrates seamlessly with different transformations like `jax.jit` and `jax.vmap` permitting for environment friendly and scalable computation.
• Reverse-Mode Differentiation(Backpropagation):   JAX’s auto-diff makes use of reverse-mode differentiation for scaler-output capabilities, which is very efficient for deep studying duties.

import jax.numpy as jnp
from jax import grad, value_and_grad


# Outline a easy neural community layer
def layer(params, x):
    weight, bias = params
    return jnp.dot(x, weight) + bias


# Outline a scalar-valued loss perform
def loss_fn(params, x):
    output = layer(params, x)
    return jnp.sum(output)  # Decreasing to a scalar


# Get each the output and gradient
layer_grad = grad(loss_fn, argnums=0)  # Gradient with respect to params
layer_value_and_grad = value_and_grad(loss_fn, argnums=0)  # Each worth and gradient

# Instance utilization
key = jax.random.PRNGKey(0)
x = jax.random.regular(key, (3, 4))
weight = jax.random.regular(key, (4, 2))
bias = jax.random.regular(key, (2,))

# Compute gradients
grads = layer_grad((weight, bias), x)
output, grads = layer_value_and_grad((weight, bias), x)

# A number of derivatives are simple
twice_grad = grad(grad(jnp.sin))
x = jnp.array(2.0)
print(f"Second spinoff of sin at x=2: {twice_grad(x)}")

Output:

Second derivatives of sin at x=2: -0.9092974066734314

Effectiveness in JAX

• Effectivity:  JAX’s computerized differentiation is very environment friendly because of its integration with XLA, permitting for optimization on the machine code stage.
• Composability:  The power to mix completely different transformations makes JAX a robust instrument for constructing advanced machine studying pipelines and Neural Networks structure comparable to CNN, RNN, and Transformers.
• Ease of Use: JAX’s syntax for autodiff is straightforward and intuitive, enabling customers to compute gradient with out delving into the main points of XLA and sophisticated library APIs.

JAX Vectorize Mapping

In JAX, `vmap` is a robust perform that mechanically vectorizes computations, permitting you to use a perform over batches of knowledge with out manually writing loops. It maps a perform over an array axis (or a number of axes) and evaluates it effectively in parallel, which may result in vital efficiency enhancements.

How vmap Works in JAX?

The vmap perform automates the method of making use of a perform to every ingredient alongside a specified axis of an enter array whereas preserving the effectivity of the computation. It transforms the given perform to just accept batched inputs and execute the computation in a vectorized method.

As a substitute of utilizing express loops, vmap permits operations to be carried out in parallel by vectorizing over an enter axis. This leverages the {hardware}’s functionality to carry out SIMD (Single Instruction, A number of Knowledge) operations, which may end up in substantial speed-ups.

Key Options of vmap

• Automated Vectorization:   vamp automates the batching of computations, making it easy to parallel code over batch dimensions with out altering the unique perform logic.
• Composability with different Transformations:    It really works seamlessly with different JAX transformations, comparable to jax.grad for differentiation and jax.jit for Simply-In-Time compilation, permitting for extremely optimized and versatile code.
• Dealing with A number of Batch Dimensions:   vmap helps mapping over a number of enter arrays or axes, making it versatile for varied use circumstances like processing multi-dimensional knowledge or a number of variables concurrently.

import jax.numpy as jnp
from jax import vmap


# A perform that works on single inputs
def single_input_fn(x):
    return jnp.sin(x) + jnp.cos(x)


# Vectorize it to work on batches
batch_fn = vmap(single_input_fn)

# Examine efficiency
x = jnp.arange(1000)

# With out vmap (utilizing a listing comprehension)
result1 = jnp.array([single_input_fn(xi) for xi in x])

# With vmap
result2 = batch_fn(x)  # A lot sooner!


# Vectorizing a number of arguments
def two_input_fn(x, y):
    return x * jnp.sin(y)


# Vectorize over each inputs
vectorized_fn = vmap(two_input_fn, in_axes=(0, 0))

# Or vectorize over simply the primary enter
partially_vectorized_fn = vmap(two_input_fn, in_axes=(0, None))


# print
print(result1.form)
print(result2.form)
print(partially_vectorized_fn(x, y).form)

Output:

(1000,)
(1000,)
(1000,3)

Effectiveness of vmap in JAX

• Efficiency Enhancements: By vectorizing computations, vmap can considerably pace up execution by leveraging parallel processing capabilities of contemporary {hardware} like GPUs, and TPUs(Tensor processing items).
• Cleaner Code: It permits for extra concise and readable code by eliminating the necessity for guide loops.
• Compatibility with JAX and Autodiff: vmap may be mixed with computerized differentiation (jax.grad), permitting for the environment friendly computation of derivatives over batches of knowledge.

When to Use Every Transformation

Utilizing @jit when:

• Your perform is named a number of occasions with comparable enter shapes.
• The perform accommodates heavy numerical computations.

Use grad when:

• You want derivatives for optimization.
• Implementing machine studying algorithms
• Fixing differential equations for simulations

Use vmap when:

• Processing batches of knowledge with.
• Parallelizing computations
• Avoiding express loops

Matrix Operations and Linear Algebra Utilizing JAX

JAX offers complete assist for matrix operations and linear algebra, making it appropriate for scientific computing, machine studying, and numerical optimization duties. JAX’s linear algebra capabilities are just like these present in libraries like NumPY however with extra options comparable to computerized differentiation and Simply-In-Time compilation for optimized efficiency.

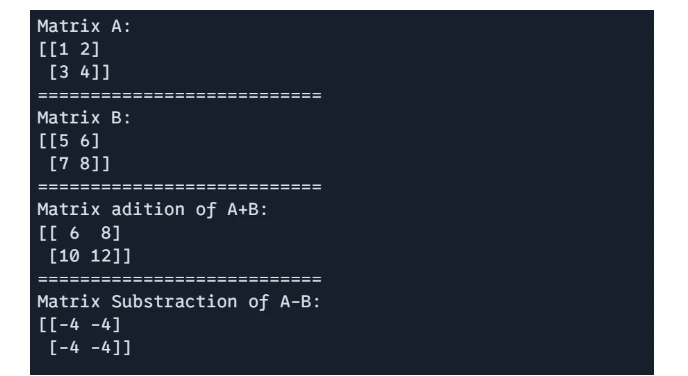
Matrix Addition and Subtraction

These operation are carried out element-wise matrices of the identical form.

# 1 Matrix Addition and Subtraction:

import jax.numpy as jnp

A = jnp.array([[1, 2], [3, 4]])
B = jnp.array([[5, 6], [7, 8]])

# Matrix addition
C = A + B
# Matrix subtraction
D = A - B

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix B: n{B}")
print("===========================")
print(f"Matrix adition of A+B: n{C}")
print("===========================")
print(f"Matrix Substraction of A-B: n{D}")

Output:

Matrix Multiplication

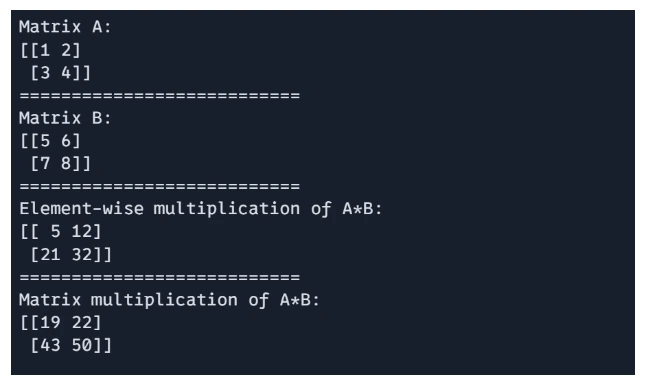
JAX assist each element-wise multiplication and dor product-based matrix multiplication.

# Ingredient-wise multiplication
E = A * B

# Matrix multiplication (dot product)
F = jnp.dot(A, B)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix B: n{B}")
print("===========================")
print(f"Ingredient-wise multiplication of A*B: n{E}")
print("===========================")
print(f"Matrix multiplication of A*B: n{F}")

Output:

Matrix Transpose

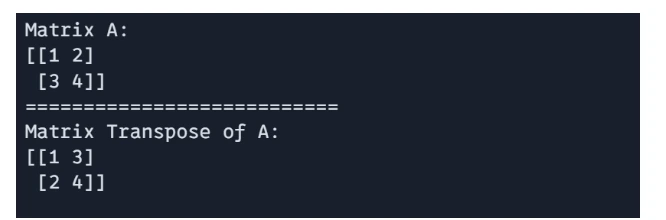
The transpose of a matrix may be obtained utilizing `jnp.transpose()`

# Matric Transpose
G = jnp.transpose(A)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix Transpose of A: n{G}")

Output:

Matrix Inverse

JAX offers perform for matrix inversion utilizing `jnp.linalg.inv()`

# Matric Inversion
H = jnp.linalg.inv(A)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix Inversion of A: n{H}")

Output:

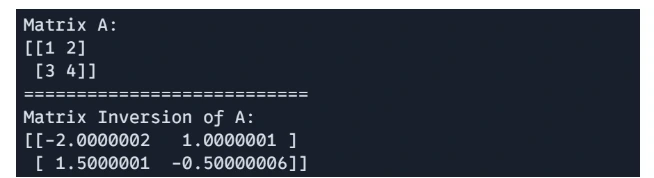
Matrix Determinant

Determinant of a matrix may be calculate utilizing `jnp.linalg.det()`.

# matrix determinant
det_A = jnp.linalg.det(A)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix Determinant of A: n{det_A}")

Output:

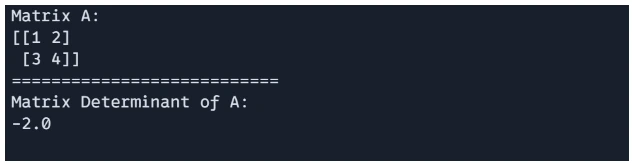
Matrix Eigenvalues and Eigenvectors

You possibly can compute the eigenvalues and eigenvectors of a matrix utilizing `jnp.linalg.eigh()`

# Eigenvalues and Eigenvectors
import jax.numpy as jnp

A = jnp.array([[1, 2], [3, 4]])
eigenvalues, eigenvectors = jnp.linalg.eigh(A)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Eigenvalues of A: n{eigenvalues}")
print("===========================")
print(f"Eigenvectors of A: n{eigenvectors}")

Output:

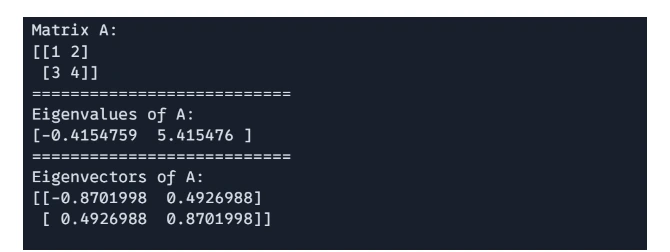
Matrix Singular Worth Decomposition

SVD is supported by way of `jnp.linalg.svd`, helpful in dimensionality discount and matrix factorization.

# Singular Worth Decomposition(SVD)

import jax.numpy as jnp

A = jnp.array([[1, 2], [3, 4]])
U, S, V = jnp.linalg.svd(A)

print(f"Matrix A: n{A}")
print("===========================")
print(f"Matrix U: n{U}")
print("===========================")
print(f"Matrix S: n{S}")
print("===========================")
print(f"Matrix V: n{V}")

Output:

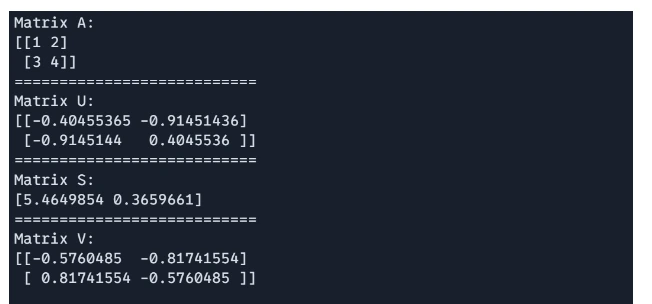
Fixing System of Linear Equations

To resolve a system of linear equation Ax = b, we use `jnp.linalg.resolve()`, the place A is a sq. matrix and b is a vector or matrix of the identical variety of rows.

# Fixing system of linear equations
import jax.numpy as jnp

A = jnp.array([[2.0, 1.0], [1.0, 3.0]])
b = jnp.array([5.0, 6.0])
x = jnp.linalg.resolve(A, b)

print(f"Worth of x: {x}")

Output:

Worth of x: [1.8 1.4]

Computing the Gradient of a Matrix Operate

Utilizing JAX’s computerized differentiation, you may compute the gradient of a scalar perform with respect to a matrix.
We are going to calculate gradient of the under perform and values of X

Operate

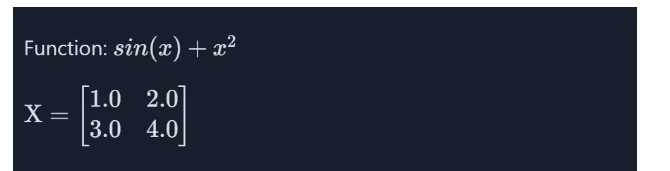
# Computing the Gradient of a Matrix Operate
import jax
import jax.numpy as jnp


def matrix_function(x):
    return jnp.sum(jnp.sin(x) + x**2)


# Compute the grad of the perform
grad_f = jax.grad(matrix_function)

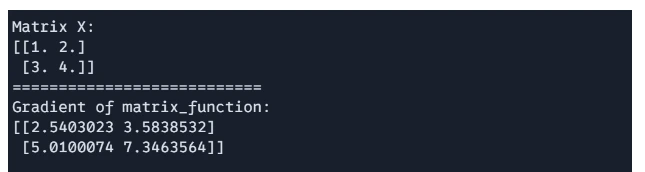
X = jnp.array([[1.0, 2.0], [3.0, 4.0]])
gradient = grad_f(X)

print(f"Matrix X: n{X}")
print("===========================")
print(f"Gradient of matrix_function: n{gradient}")

Output:

These most helpful perform of JAX utilized in numerical computing, machine studying, and physics calculation. There are lots of extra left so that you can discover.

Scientific Computing with JAX

JAX’s highly effective libraries for scientific computing, JAX is finest for scientific computing for its advance options comparable to JIT compilation, computerized differentiation, vectorization, parallelization, and GPU-TPU acceleration. JAX’s capacity to assist excessive efficiency computing makes it appropriate for a variety of scientific functions, together with physics simulations, machine studying, optimization and numerical evaluation.

We are going to discover an Optimization Drawback on this part.

Optimization Issues

Allow us to undergo the optimization issues steps under:

Step1: Outline the perform to attenuate(or the issue)

# Outline a perform to attenuate (e.g., Rosenbrock perform)

@jit

def rosenbrock(x):

    return sum(100.0 * (x[1:] - x[:-1] ** 2.0) ** 2.0 + (1 - x[:-1]) ** 2.0)

Right here, the Rosenbrock perform is outlined, which is a typical check downside in optimization. The perform takes an array x as enter and computes a valie that represents how far x is from the perform’s international minimal. The @jit decorator is used to allow Jut-In-Time compilation, which pace up the computation by compiling the perform to run effectively on CPUs and GPUs.

Step2: Gradient Descent Step Implementation

# Gradient descent optimization

@jit

def gradient_descent_step(x, learning_rate):

    return x - learning_rate * grad(rosenbrock)(x)

This perform performs a single step of the gradient descent optimization. The gradient of the Rosenbrock perform is calculated utilizing grad(rosenbrock)(x), which offers the spinoff with respects to x. The brand new worth of x is up to date by subtraction the gradient scaled by a learning_rate.The @jit is doing the identical as earlier than.

Step3: Operating the Optimization Loop

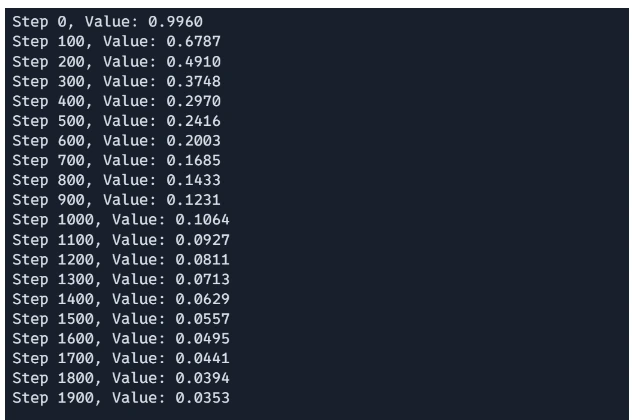
# Optimize
x = jnp.array([0.0, 0.0])  # Start line

learning_rate = 0.001

for i in vary(2000):

    x = gradient_descent_step(x, learning_rate)

    if i % 100 == 0:

        print(f"Step {i}, Worth: {rosenbrock(x):.4f}")

The optimization loop initializes the start line x and performs 1000 iterations of gradient descent. In every iteration, the gradient_descent_step perform updates based mostly on the present gradient. Each 100 steps, the present step quantity and the worth of the Rosenbrock perform at x are printed, offering the progress of the optimization.

Output:

Fixing Actual-world physics downside with JAX

We are going to simulate a bodily system the movement of a damped harmonic oscillator, which fashions issues like a mass-spring system with friction, shock absorbers in automobiles, or oscillation in electrical circuits. Is it not good? Let’s do it.

Step1: Parameters Definition

import jax
import jax.numpy as jnp


# Outline parameters
mass = 1.0  # Mass of the thing (kg)
damping = 0.1  # Damping coefficient (kg/s)
spring_constant = 1.0  # Spring fixed (N/m)

# Outline time step and whole time
dt = 0.01  # Time step (s)
num_steps = 3000  # Variety of steps

The mass, damping coefficient, and spring fixed are outlined. These decide the bodily properties of the damped harmonic oscillator.

Step2: ODE Definition

# Outline the system of ODEs
def damped_harmonic_oscillator(state, t):
    """Compute the derivatives for a damped harmonic oscillator.

    state: array containing place and velocity [x, v]
    t: time (not used on this autonomous system)
    """
    x, v = state
    dxdt = v
    dvdt = -damping / mass * v - spring_constant / mass * x
    return jnp.array([dxdt, dvdt])

  The damped harmonic oscillator perform defines the derivatives of the place and velocity of the oscillator, representing the dynamical system.

Step3: Euler’s Technique

# Resolve the ODE utilizing Euler's methodology
def euler_step(state, t, dt):
    """Carry out one step of Euler's methodology."""
    derivatives = damped_harmonic_oscillator(state, t)
    return state + derivatives * dt

A easy numerical methodology is used to unravel the ODE. It approximates the state on the subsequent time step on the premise of the present state and spinoff.

Step4: Time Evolution Loops

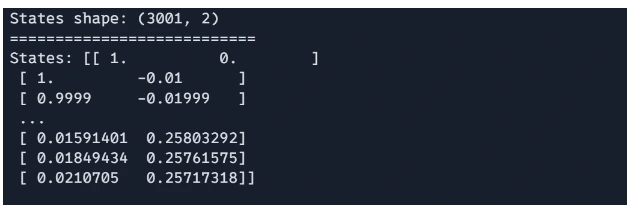
# Preliminary state: [position, velocity]
initial_state = jnp.array([1.0, 0.0])  # Begin with the mass at x=1, v=0

# Time evolution
states = [initial_state]
time = 0.0
for step in vary(num_steps):
    next_state = euler_step(states[-1], time, dt)
    states.append(next_state)
    time += dt

# Convert the checklist of states to a JAX array for evaluation
states = jnp.stack(states)

The loop iterates by means of the desired variety of time steps, updating the state at every step utilizing Euler’s methodology.

Output:

Step5: Plotting The Outcomes

Lastly, we will plot the outcomes to visualise the conduct of the damped harmonic oscillator.

# Plotting the outcomes
import matplotlib.pyplot as plt

plt.model.use("ggplot")

positions = states[:, 0]
velocities = states[:, 1]
time_points = jnp.arange(0, (num_steps + 1) * dt, dt)

plt.determine(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.plot(time_points, positions, label="Place")
plt.xlabel("Time (s)")
plt.ylabel("Place (m)")
plt.legend()

plt.subplot(2, 1, 2)
plt.plot(time_points, velocities, label="Velocity", coloration="orange")
plt.xlabel("Time (s)")
plt.ylabel("Velocity (m/s)")
plt.legend()

plt.tight_layout()
plt.present()

Output:

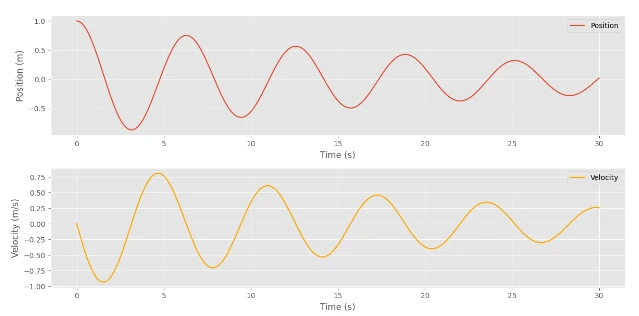
I do know you’re desirous to see how the Neural Community may be constructed with JAX. So, let’s dive deep into it.

Right here, you may see that the Values had been minimized progressively.

Constructing Neural Networks with JAX

JAX is a robust library that mixes high-performance numerical computing with the benefit of utilizing NumPy-like syntax. This part will information you thru the method of establishing a neural community utilizing JAX, leveraging its superior options for computerized differentiation and just-in-time compilation to optimize efficiency.

Step1: Importing Libraries

Earlier than we dive into constructing our neural community, we have to import the required libraries. JAX offers a set of instruments for creating environment friendly numerical computations, whereas extra libraries will help with optimization and visualization of our outcomes.

import jax
import jax.numpy as jnp
from jax import grad, jit
from jax.random import PRNGKey, regular
import optax  # JAX's optimization library
import matplotlib.pyplot as plt

Step2: Creating the Mannequin Layers

Creating efficient mannequin layers is essential in defining the structure of our neural community. On this step, we’ll initialize the parameters for our dense layers, guaranteeing that our mannequin begins with well-defined weights and biases for efficient studying.

def init_layer_params(key, n_in, n_out):
    """Initialize parameters for a single dense layer"""
    key_w, key_b = jax.random.cut up(key)
    # He initialization
    w = regular(key_w, (n_in, n_out)) * jnp.sqrt(2.0 / n_in)  
    b = regular(key_b, (n_out,)) * 0.1
    return (w, b)
    
def relu(x):
    """ReLU activation perform"""
    return jnp.most(0, x)
    

• Initializing Operate: init_layer_params initializes weights(w) and biases (b) for dense layers utilizing He initialization for weight and a small worth for biases. He or Kaiming He initialization works higher for layers with ReLu activation capabilities, there are different well-liked initialization strategies comparable to Xavier initialization which works higher for layers with sigmoid activation.
• Activation Operate: The relu perform applies the ReLu activation perform to the inputs which set destructive values to zero.

Step3: Defining the Ahead Go

The ahead cross is the cornerstone of a neural community, because it dictates how enter knowledge flows by means of the community to supply an output. Right here, we are going to outline a way to compute the output of our mannequin by making use of transformations to the enter knowledge by means of the initialized layers.

def ahead(params, x):
    """Ahead cross for a two-layer neural community"""
    (w1, b1), (w2, b2) = params
    # First layer
    h1 = relu(jnp.dot(x, w1) + b1)
    # Output layer
    logits = jnp.dot(h1, w2) + b2
    return logits
    

• Ahead Go: ahead performs a ahead cross by means of a two-layer neural community, computing the output (logits) by making use of a linear transformation adopted by ReLu, and different linear transformations.

Step4: Defining the loss perform

A well-defined loss perform is crucial for guiding the coaching of our mannequin. On this step, we are going to implement the imply squared error (MSE) loss perform, which measures how nicely the expected outputs match the goal values, enabling the mannequin to be taught successfully.

def loss_fn(params, x, y):
    """Imply squared error loss"""
    pred = ahead(params, x)
    return jnp.imply((pred - y) ** 2)

• Loss Operate: loss_fn calculates the imply squared error (MSE) loss between the expected logits and the goal labels (y).

Step5: Mannequin Initialization

With our mannequin structure and loss perform outlined, we now flip to mannequin initialization. This step includes organising the parameters of our neural community, guaranteeing that every layer is able to start the coaching course of with random however appropriately scaled weights and biases.

def init_model(rng_key, input_dim, hidden_dim, output_dim):
    key1, key2 = jax.random.cut up(rng_key)
    params = [
        init_layer_params(key1, input_dim, hidden_dim),
        init_layer_params(key2, hidden_dim, output_dim),
    ]
    return params
    

• Mannequin Initialization: init_model initializes the weights and biases for each layers of the neural networks. It makes use of two separate random keys for every layer;’s parameter initialization.

Step6: Coaching Step

Coaching a neural community includes iterative updates to its parameters based mostly on the computed gradients of the loss perform. On this step, we are going to implement a coaching perform that applies these updates effectively, permitting our mannequin to be taught from the info over a number of epochs.

@jit
def train_step(params, opt_state, x_batch, y_batch):
    loss, grads = jax.value_and_grad(loss_fn)(params, x_batch, y_batch)
    updates, opt_state = optimizer.replace(grads, opt_state)
    params = optax.apply_updates(params, updates)
    return params, opt_state, loss

• Coaching Step: the train_step perform performs a single gradient descent replace.
• It calculates the loss and gradients utilizing value_and_grad, which computes each the perform values and different gradients.
• The optimizer updates are calculated, and the mannequin parameters are up to date accordingly.
• The is JIT-compiled for efficiency.

Step7: Knowledge and Coaching Loop

To coach our mannequin successfully, we have to generate appropriate knowledge and implement a coaching loop. This part will cowl find out how to create artificial knowledge for our instance and find out how to handle the coaching course of throughout a number of batches and epochs.

# Generate some instance knowledge
key = PRNGKey(0)
x_data = regular(key, (1000, 10))  # 1000 samples, 10 options
y_data = jnp.sum(x_data**2, axis=1, keepdims=True)  # Easy nonlinear perform

# Initialize mannequin and optimizer
params = init_model(key, input_dim=10, hidden_dim=32, output_dim=1)
optimizer = optax.adam(learning_rate=0.001)
opt_state = optimizer.init(params)

# Coaching loop
batch_size = 32
num_epochs = 100
num_batches = x_data.form[0] // batch_size

# Arrays to retailer epoch and loss values
epoch_array = []
loss_array = []

for epoch in vary(num_epochs):
    epoch_loss = 0.0
    for batch in vary(num_batches):
        idx = jax.random.permutation(key, batch_size)
        x_batch = x_data[idx]
        y_batch = y_data[idx]
        params, opt_state, loss = train_step(params, opt_state, x_batch, y_batch)
        epoch_loss += loss

    # Retailer the typical loss for the epoch
    avg_loss = epoch_loss / num_batches
    epoch_array.append(epoch)
    loss_array.append(avg_loss)

    if epoch % 10 == 0:
        print(f"Epoch {epoch}, Loss: {avg_loss:.4f}")

• Knowledge Era: Random coaching knowledge (x_data) and corresponding goal (y_data) values are created.    Mannequin and Optimizer Initialization: The mannequin parameters and optimizer state are initialized.
• Coaching Loop: The networks are educated over a specified variety of epochs, utilizing mini-batch gradient descent.       
• Coaching loops iterate over batches, performing gradient updates utilizing the train_step perform.  The typical loss per epoch is calculated and saved. It prints the epoch quantity and the typical loss.

Step8: Plotting the Outcomes

Visualizing the coaching outcomes is vital to understanding the efficiency of our neural community. On this step, we are going to plot the coaching loss over epochs to watch how nicely the mannequin is studying and to determine any potential points within the coaching course of.

# Plot the outcomes
plt.plot(epoch_array, loss_array, label="Coaching Loss")
plt.xlabel("Epoch")
plt.ylabel("Loss")
plt.title("Coaching Loss over Epochs")
plt.legend()
plt.present()

These examples display how JAX combines excessive efficiency with clear, readable code. The practical programming model inspired by JAX makes it simple to compose operations and apply transformations.

Output:

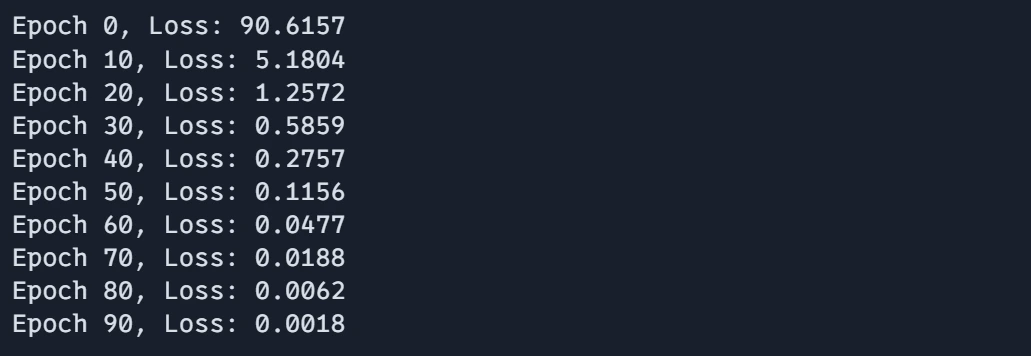
Plot:

These examples display how JAX combines excessive efficiency with clear, readable code. The practical programming model inspired by JAX makes it simple to compose operations and apply transformations.

Greatest Follow and Suggestions

In constructing neural networks, adhering to finest practices can considerably improve efficiency and maintainability. This part will focus on varied methods and suggestions for optimizing your code and enhancing the general effectivity of your JAX-based fashions.

Efficiency Optimization

Optimizing efficiency is crucial when working with JAX, because it permits us to totally leverage its capabilities. Right here, we are going to discover completely different methods for enhancing the effectivity of our JAX capabilities, guaranteeing that our fashions run as rapidly as potential with out sacrificing readability.

JIT Compilation Greatest Practices

Simply-In-Time (JIT) compilation is without doubt one of the standout options of JAX, enabling sooner execution by compiling capabilities at runtime. This part will define finest practices for successfully utilizing JIT compilation, serving to you keep away from frequent pitfalls and maximize the efficiency of your code.

Dangerous Operate

import jax
import jax.numpy as jnp
from jax import jit
from jax import lax


# BAD: Dynamic Python management move inside JIT
@jit
def bad_function(x, n):
    for i in vary(n):  # Python loop - will likely be unrolled
        x = x + 1
    return x
    
    
print("===========================")
# print(bad_function(1, 1000)) # doesn't work
    

This perform makes use of a typical Python loop to iterate n occasions, incrementing the of x by 1 on every iteration. When compiled with jit, JAX unrolls the loop, which may be inefficient, particularly for giant n. This strategy doesn’t absolutely leverage JAX’s capabilities for efficiency.

Good Operate

# GOOD: Use JAX-native operations
@jit
def good_function(x, n):
    return x + n  # Vectorized operation


print("===========================")
print(good_function(1, 1000))

This perform does the identical operation, nevertheless it makes use of a vectorized operation (x+n) as an alternative of a loop. This strategy is rather more environment friendly as a result of JAX can higher optimize the computation when expressed as a single vectorized operation.

Greatest Operate

# BETTER: Use scan for loops


@jit
def best_function(x, n):
    def body_fun(i, val):
        return val + 1

    return lax.fori_loop(0, n, body_fun, x)


print("===========================")
print(best_function(1, 1000))

This strategy makes use of `jax.lax.fori_loop`, which is a JAX-native technique to implement loops effectively. The `lax.fori_loop` performs the identical increment operation because the earlier perform, nevertheless it does so utilizing a compiled loop construction. The body_fn perform defines the operation for every iteration, and `lax.fori_loop` executes it from o to n. This methodology is extra environment friendly than unrolling loops and is particularly appropriate for circumstances the place the variety of iterations isn’t recognized forward of time.

Output:

===========================
===========================
1001
===========================
1001

The code demonstrates completely different approaches to dealing with loops and management move inside JAX’s jit-complied capabilities.

Reminiscence Administration

Environment friendly reminiscence administration is essential in any computational framework, particularly when coping with giant datasets or advanced fashions. This part will focus on frequent pitfalls in reminiscence allocation and supply methods for optimizing reminiscence utilization in JAX.

Inefficient Reminiscence Administration

# BAD: Creating giant momentary arrays
@jit
def inefficient_function(x):
    temp1 = jnp.energy(x, 2)  # Short-term array
    temp2 = jnp.sin(temp1)  # One other momentary
    return jnp.sum(temp2)

inefficient_function(x): This perform creates a number of intermediate arrays, temp1, temp1  and at last the sum of the weather in temp2. Creating these momentary arrays may be inefficient as a result of every step allocates reminiscence and incurs computational overhead, resulting in slower execution and better reminiscence utilization.

Environment friendly Reminiscence Administration

# GOOD: Combining operations
@jit
def efficient_function(x):
    return jnp.sum(jnp.sin(jnp.energy(x, 2)))  # Single operation

This model combines all operations right into a single line of code. It computes the sine of squared parts of x straight and sums the outcomes. By combining the operation, it avoids creating intermediate arrays, lowering reminiscence footprints and enhancing efficiency.

Take a look at Code

x = jnp.array([1, 2, 3])
print(x)
print(inefficient_function(x))
print(efficient_function(x))

Output:

[1 2 3]
0.49678695
0.49678695

The environment friendly model leverages JAX’s capacity to optimize the computation graph, making the code sooner and extra memory-efficient by minimizing momentary array creation.

Debugging Methods

Debugging is a vital a part of the event course of, particularly in advanced numerical computations. On this part, we are going to focus on efficient debugging methods particular to JAX, enabling you to determine and resolve points rapidly.

Utilizing print inside JIT for Debugging

The code reveals methods for debugging inside JAX, significantly when utilizing JIT-compiled capabilities.

import jax.numpy as jnp
from jax import debug


@jit
def debug_function(x):
    # Use debug.print as an alternative of print inside JIT
    debug.print("Form of x: {}", x.form)
    y = jnp.sum(x)
    debug.print("Sum: {}", y)
    return y

# For extra advanced debugging, escape of JIT
def debug_values(x):
    print("Enter:", x)
    outcome = debug_function(x)
    print("Output:", outcome)
    return outcome
    

• debug_function(x): This perform reveals find out how to use debug.print() for debugging inside a jit compiled perform. In JAX, common Python print statements aren’t allowed inside JIT because of compilation restrictions, so debug.print() is used as an alternative.
• It prints the form of the enter array x utilizing debug.print()
• After computing the sum of the weather of x, it prints the ensuing sum utilizing debug.print()
• Lastly, the perform returns the computed sum y.
• debug_values(x) perform serves as a higher-level debugging strategy, breaking out of the JIT context for extra advanced debugging. It first prints the inputs x utilizing common print assertion. Then calls debug_function(x) to compute the outcome and at last prints the output earlier than returning the outcomes.

Output:

print("===========================")
print(debug_function(jnp.array([1, 2, 3])))
print("===========================")
print(debug_values(jnp.array([1, 2, 3])))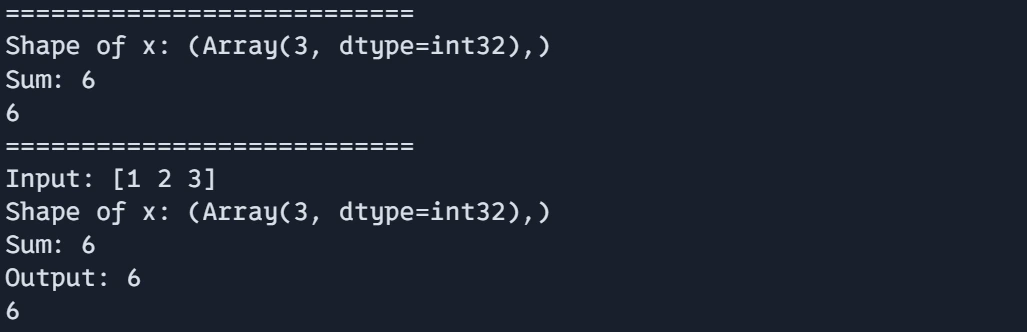

This strategy permits for a mix of in-JIT debugging with debug.print() and extra detailed debugging outdoors of JIT utilizing commonplace Python print statements.

Widespread Patterns and Idioms in JAX

Lastly, we are going to discover frequent patterns and idioms in JAX that may assist streamline your coding course of and enhance effectivity. Familiarizing your self with these practices will support in growing extra strong and performant JAX functions.

Machine Reminiscence Administration for Processing Giant Datasets

# 1. Machine Reminiscence Administration
def process_large_data(knowledge):
    # Course of in chunks to handle reminiscence
    chunk_size = 100
    outcomes = []

    for i in vary(0, len(knowledge), chunk_size):
        chunk = knowledge[i : i + chunk_size]
        chunk_result = jit(process_chunk)(chunk)
        outcomes.append(chunk_result)

    return jnp.concatenate(outcomes)


def process_chunk(chunk):
    chunk_temp = jnp.sqrt(chunk)
    return chunk_temp

This perform processes giant datasets in chunks to keep away from overwhelming gadget reminiscence.   

It units chunk_size to 100 and iterates over the info increments of the chunk dimension, processing every chunk individually.   

For every chunk, the perform makes use of jit(process_chunk) to JIT-compile the processing operation, which improves efficiency by compiling it forward of time.   

The results of every chunk is concatenated right into a single array utilizing jnp.concatenated(outcome) to type a single checklist.

Output:

print("===========================")
knowledge = jnp.arange(10000)
print(knowledge.form)

print("===========================")
print(knowledge)

print("===========================")
print(process_large_data(knowledge))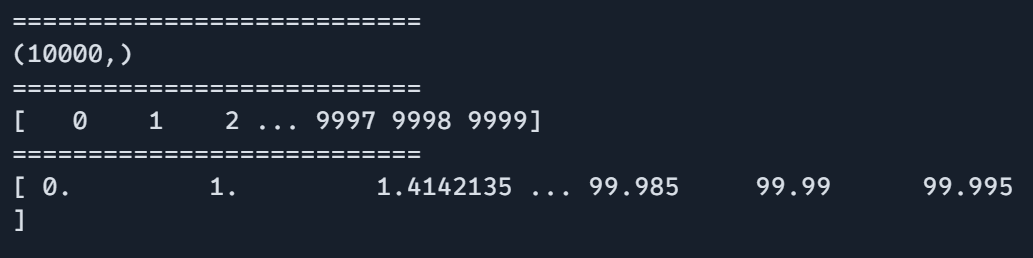

Dealing with Random Seed for Reproducibility and Higher Knowledge Era

The perform create_traing_state() demonstrates managing random quantity mills (RNGs) in JAX, which is crucial for reproducibility and constant outcomes.

# 2. Dealing with Random Seeds
def create_training_state(rng):
    # Cut up RNG for various makes use of
    rng, init_rng = jax.random.cut up(rng)
    params = init_network(init_rng)

    return params, rng  # Return new RNG for subsequent use
    

It begins with an preliminary RNG (rng) and splits it into two new RNGs utilizing jax.random.cut up(). Cut up RNGs carry out completely different duties: `init_rng` initializes community parameters, and the up to date RNG returns for subsequent operations.

The perform returns each the initialized community parameters and the brand new RNG for additional use, guaranteeing correct dealing with of random states throughout completely different steps.

Now check the code utilizing mock knowledge

def init_network(rng):
    # Initialize community parameters
    return {
        "w1": jax.random.regular(rng, (784, 256)),
        "b1": jax.random.regular(rng, (256,)),
        "w2": jax.random.regular(rng, (256, 10)),
        "b2": jax.random.regular(rng, (10,)),
    }


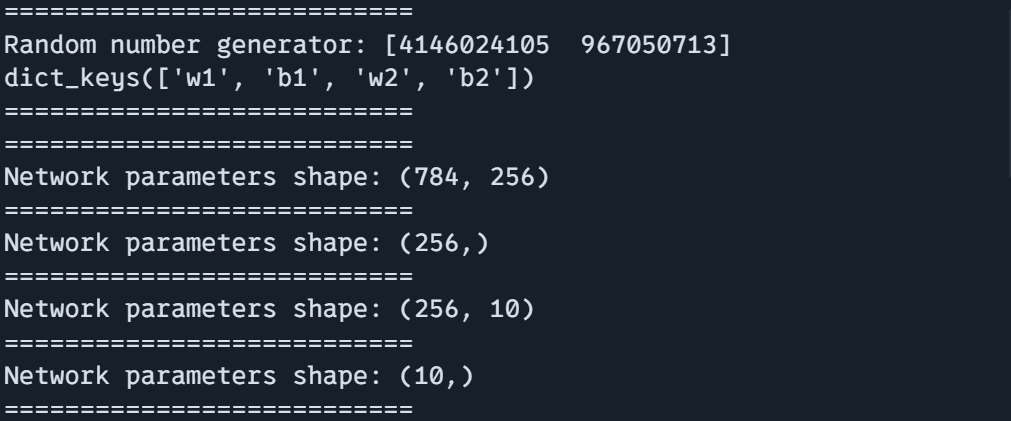
print("===========================")

key = jax.random.PRNGKey(0)
params, rng = create_training_state(key)


print(f"Random quantity generator: {rng}")

print(params.keys())

print("===========================")


print("===========================")
print(f"Community parameters form: {params['w1'].form}")

print("===========================")
print(f"Community parameters form: {params['b1'].form}")
print("===========================")
print(f"Community parameters form: {params['w2'].form}")

print("===========================")
print(f"Community parameters form: {params['b2'].form}")


print("===========================")
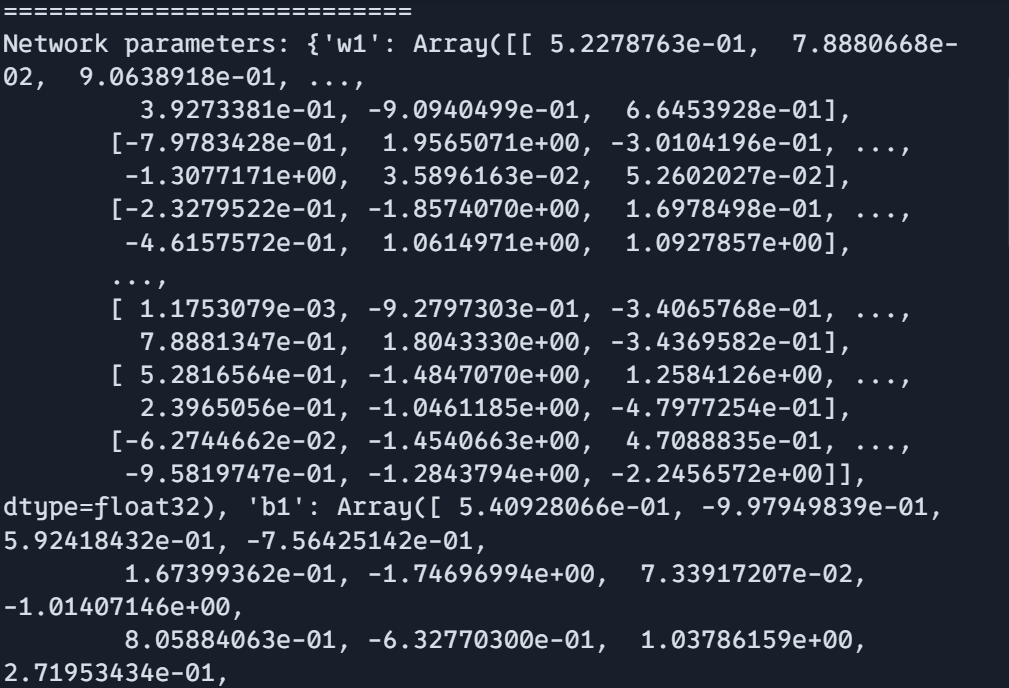
print(f"Community parameters: {params}")

Output:

Utilizing Static Arguments in JIT

def g(x, n):
    i = 0
    whereas i < n:
        i += 1
    return x + i


g_jit_correct = jax.jit(g, static_argnames=["n"])
print(g_jit_correct(10, 20))

Output:

30

You need to use a static argument if JIT compiles the perform with the identical arguments every time. This may be helpful for the efficiency optimization of JAX capabilities.   

from functools import partial


@partial(jax.jit, static_argnames=["n"])
def g_jit_decorated(x, n):
    i = 0
    whereas i < n:
        i += 1
    return x + i


print(g_jit_decorated(10, 20))

If You wish to use static arguments in JIT as a decorator you need to use jit inside functools. partial() perform.

Output:

30

Now, we’ve realized and dived deep into many thrilling ideas and methods in JAX and general programming model.

What’s Subsequent?

• Experiment with Examples: Attempt to modify the code examples to be taught extra about JAX.    Construct a small challenge for a greater understanding of JAX’s transformations and APIs.    Implement classical Machine Studying algorithms with JAX comparable to Logistic Regression, Assist Vector Machine, and extra.
• Discover Superior Matters: Parallel computing with pmap, Customized JAX transformations,   Integration with different frameworks

All code used on this article is right here

Conclusion

JAX is a robust instrument that gives a variety of capabilities for machine studying, Deep Studying, and scientific computing. Begin with fundamentals, experimenting, and get assist from JAX’s lovely documentation and neighborhood. There are such a lot of issues to be taught and it’ll not be realized by simply studying others’ code you need to do it by yourself. So, begin making a small challenge in the present day in JAX. The secret’s to Maintain Going, be taught on the best way.

Key Takeaways

• Acquainted NumPY-like interface and APIs make studying JAX simple for novices. Most NumPY code works with minimal modifications.
• JAX encourages clear practical programming patterns that result in cleaner, extra maintainable code and upgradation. However If builders need JAX absolutely appropriate with Object Oriented paradigm.
• What makes JAX’s options so highly effective is computerized differentiation and JAX’s JIT compilation, which makes it environment friendly for large-scale knowledge processing.
• JAX excels in scientific computing, optimization, neural networks, simulation, and machine studying which makes developer simple to make use of on their respective challenge.

Ceaselessly Requested Questions

The media proven on this article is just not owned by Analytics Vidhya and is used on the Writer’s discretion.