The Consideration Mechanism is commonly related to the transformer structure, however it was already utilized in RNNs. In Machine Translation or MT (e.g., English-Italian) duties, whenever you need to predict the subsequent Italian phrase, you want your mannequin to focus, or concentrate, on an important English phrases which can be helpful to make an excellent translation.

I can’t go into particulars of RNNs, however consideration helped these fashions to mitigate the vanishing gradient drawback and to seize extra long-range dependencies amongst phrases.
At a sure level, we understood that the one necessary factor was the eye mechanism, and your complete RNN structure was overkill. Therefore, Consideration is All You Want!
Self-Consideration in Transformers
Classical consideration signifies the place phrases within the output sequence ought to focus consideration in relation to the phrases in enter sequence. That is necessary in sequence-to-sequence duties like MT.
The self-attention is a selected sort of consideration. It operates between any two parts in the identical sequence. It supplies info on how “correlated” the phrases are in the identical sentence.
For a given token (or phrase) in a sequence, self-attention generates a listing of consideration weights comparable to all different tokens within the sequence. This course of is utilized to every token within the sentence, acquiring a matrix of consideration weights (as within the image).
That is the overall thought, in follow issues are a bit extra sophisticated as a result of we need to add many learnable parameters to our neural community, let’s see how.
Okay, V, Q representations
Our mannequin enter is a sentence like “my title is Marcello Politi”. With the method of tokenization, a sentence is transformed into a listing of numbers like [2, 6, 8, 3, 1].
Earlier than feeding the sentence into the transformer we have to create a dense illustration for every token.
The right way to create this illustration? We multiply every token by a matrix. The matrix is realized throughout coaching.
Let’s add some complexity now.
For every token, we create 3 vectors as a substitute of 1, we name these vectors: key, worth and question. (We see later how we create these 3 vectors).

Conceptually these 3 tokens have a specific that means:
- The vector key represents the core info captured by the token
- The vector worth captures the complete info of a token
- The vector question, it’s a query in regards to the token relevance for the present activity.
So the concept is that we give attention to a specific token i , and we need to ask what’s the significance of the opposite tokens within the sentence relating to the token i we’re considering.
Which means we take the vector q_i (we ask a query relating to i) for token i, and we do some mathematical operations with all the opposite tokens k_j (j!=i). That is like questioning at first look what are the opposite tokens within the sequence that look actually necessary to grasp the that means of token i.
What is that this magical mathematical operation?
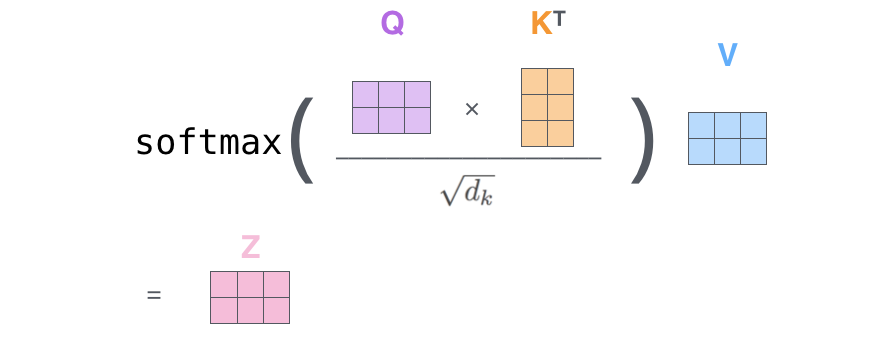
We have to multiply (dot-product) the question vector by the important thing vectors and divide by a scaling issue. We do that for every k_j token.
On this method, we get hold of a rating for every pair (q_i, k_j). We make this record turn out to be a likelihood distribution by making use of a softmax operation on it. Nice now we’ve got obtained the consideration weights!
With the eye weights, we all know what’s the significance of every token k_j to for undestandin the token i. So now we multiply the worth vector v_j related to every token per its weight and we sum the vectors. On this method we get hold of the ultimate context-aware vector of token_i.
If we’re computing the contextual dense vector of token_1 we calculate:
z1 = a11*v1 + a12*v2 + … + a15*v5
The place a1j are the pc consideration weights, and v_j are the worth vectors.
Performed! Nearly…
I didn’t cowl how we obtained the vectors okay, v and q of every token. We have to outline some matrices w_k, w_v and w_q in order that after we multiply:
- token * w_k -> okay
- token * w_q -> q
- token * w_v -> v
These 3 matrices are set at random and are realized throughout coaching, because of this we’ve got many parameters in trendy fashions resembling LLMs.
Multi-head Self-Consideration in Transformers (MHSA)
Are we certain that the earlier self-attention mechanism is ready to seize all necessary relationships amongst tokens (phrases) and create dense vectors of these tokens that basically make sense?
It may really not work all the time completely. What if to mitigate the error we re-run your complete factor 2 instances with new w_q, w_k and w_v matrices and someway merge the two dense vectors obtained? On this method perhaps one self-attention managed to seize some relationship and the opposite managed to seize another relationship.
Properly, that is what precisely occurs in MHSA. The case we simply mentioned incorporates two heads as a result of it has two units of w_q, w_k and w_v matrices. We will have much more heads: 4, 8, 16 and many others.
The one sophisticated factor is that each one these heads are managed in parallel, we course of the all in the identical computation utilizing tensors.

The best way we merge the dense vectors of every head is easy, we concatenate them (therefore the dimension of every vector shall be smaller in order that when concat them we get hold of the unique dimension we needed), and we go the obtained vector by means of one other w_o learnable matrix.
Fingers-on
Suppose you could have a sentence. After tokenization, every token (phrase for simplicity) corresponds to an index (quantity):
Earlier than feeding the sentence into the transofrmer we have to create a dense illustration for every token.
The right way to create these illustration? We multiply every token per a matrix. This matrix is realized throughout coaching.
Let’s construct this embedding matrix.
If we multiply our tokenized sentence with the embeddings, we get hold of a dense illustration of dimension 16 for every token
To be able to use the eye mechanism we have to create 3 new We outline 3 matrixes w_q, w_k and w_v. Once we multiply one enter token time the w_q we get hold of the vector q. Identical with w_k and w_v.
Compute consideration weights
Let’s now compute the eye weights for less than the primary enter token of the sentence.
We have to multiply the question vector related to token1 (query_1) with all of the keys of the opposite vectors.
So now we have to compute all of the keys (key_2, key_2, key_4, key_5). However wait, we are able to compute all of those in a single time by multiplying the sentence_embed instances the w_k matrix.
Let’s do the identical factor with the values
Let’s compute the primary a part of the attions components.
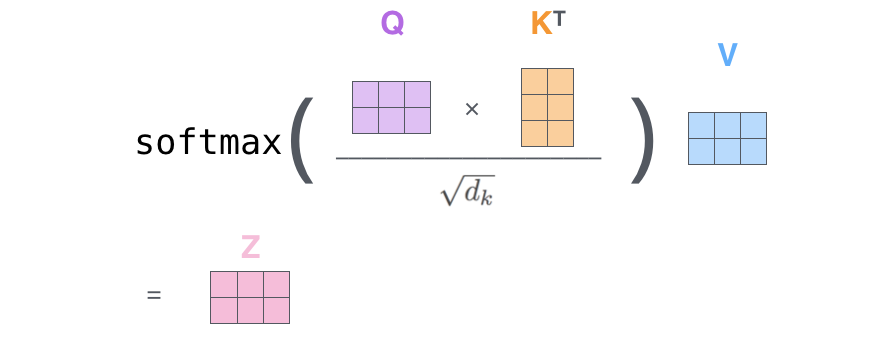
import torch.nn.useful as FWith the eye weights we all know what’s the significance of every token. So now we multiply the worth vector related to every token per its weight.
To acquire the ultimate context conscious vector of token_1.
In the identical method we may compute the context conscious dense vectors of all the opposite tokens. Now we’re all the time utilizing the identical matrices w_k, w_q, w_v. We are saying that we use one head.
However we are able to have a number of triplets of matrices, so multi-head. That’s why it’s known as multi-head consideration.
The dense vectors of an enter tokens, given in oputut from every head are at then finish concatenated and linearly reworked to get the ultimate dense vector.
Implementing MultiheadSelf-Consideration
Identical steps as earlier than…
We’ll outline a multi-head consideration mechanism with h heads (let’s say 4 heads for this instance). Every head could have its personal w_q, w_k, and w_v matrices, and the output of every head might be concatenated and handed by means of a last linear layer.
Because the output of the top might be concatenated, and we wish a last dimension of d, the dimension of every head must be d/h. Moreover every concatenated vector will go although a linear transformation, so we’d like one other matrix w_ouptut as you possibly can see within the components.
Since we’ve got 4 heads, we wish 4 copies for every matrix. As a substitute of copies, we add a dimension, which is identical factor, however we solely do one operation. (Think about stacking matrices on prime of one another, its the identical factor).
I’m utilizing for simplicity torch’s einsum. Should you’re not conversant in it try my weblog put up.
The einsum operation torch.einsum('sd,hde->hse', sentence_embed, w_query) in PyTorch makes use of letters to outline how one can multiply and rearrange numbers. Right here’s what every half means:
- Enter Tensors:
sentence_embedwith the notation'sd':srepresents the variety of phrases (sequence size), which is 5.drepresents the variety of numbers per phrase (embedding measurement), which is 16.- The form of this tensor is
[5, 16].
w_querywith the notation'hde':hrepresents the variety of heads, which is 4.drepresents the embedding measurement, which once more is 16.erepresents the brand new quantity measurement per head (d_k), which is 4.- The form of this tensor is
[4, 16, 4].
- Output Tensor:
- The output has the notation
'hse':hrepresents 4 heads.srepresents 5 phrases.erepresents 4 numbers per head.- The form of the output tensor is
[4, 5, 4].
- The output has the notation
This einsum equation performs a dot product between the queries (hse) and the transposed keys (hek) to acquire scores of form [h, seq_len, seq_len], the place:
- h -> Variety of heads.
- s and okay -> Sequence size (variety of tokens).
- e -> Dimension of every head (d_k).
The division by (d_k ** 0.5) scales the scores to stabilize gradients. Softmax is then utilized to acquire consideration weights:
Now we concatenate all of the heads of token 1
Let’s lastly multiply per the final w_output matrix as within the components above
Remaining Ideas
On this weblog put up I’ve applied a easy model of the eye mechanism. This isn’t how it’s actually applied in trendy frameworks, however my scope is to supply some insights to permit anybody an understanding of how this works. In future articles I’ll undergo your complete implementation of a transformer structure.
Comply with me on TDS should you like this text! 😁
💼 Linkedin ️| 🐦 X (Twitter) | 💻 Web site
Until in any other case famous, photos are by the creator