Bayesian Pondering in Trendy Knowledge Science

Picture by Editor | Midjourney

Bayesian pondering is a approach to make selections utilizing likelihood. It begins with preliminary beliefs (priors) and modifications them when new proof is available in (posterior). This helps in making higher predictions and selections based mostly on information. It’s essential in fields like AI and statistics the place correct reasoning is essential.

Fundamentals of Bayesian Idea

Key phrases

• Prior Chance (Prior): Represents the preliminary perception concerning the speculation.
• Chance: Measures how properly the speculation explains the proof.
• Posterior Chance (Posterior): Combines the prior likelihood and the probability.
• Proof: Updates the likelihood of the speculation.

Bayes’ Theorem

This theorem describes tips on how to replace the likelihood of a speculation based mostly on new info. It’s mathematically expressed as:

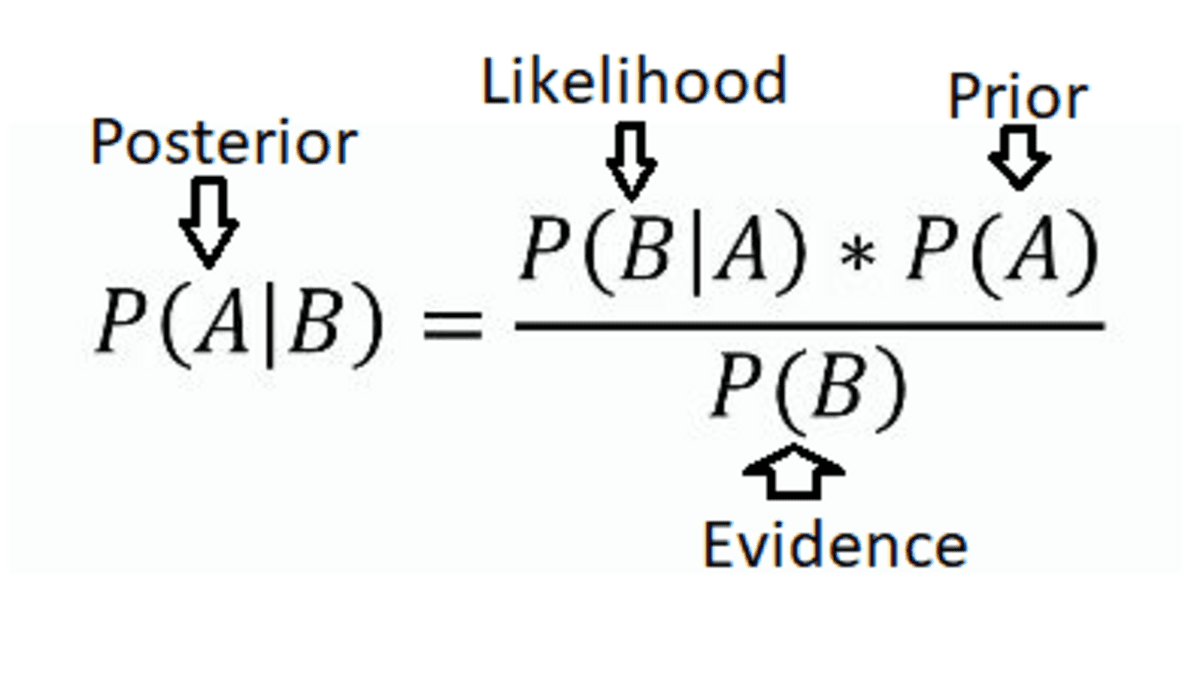
Bayes’ Theorem (Supply: Eric Castellanos Weblog)

the place:
P(A|B) is the posterior likelihood of the speculation.
P(B|A) is he probability of the proof given the speculation.
P(A) is the prior likelihood of the speculation.
P(B) is the entire likelihood of the proof.

Purposes of Bayesian Strategies in Knowledge Science

Bayesian Inference

Bayesian inference updates beliefs when issues are unsure. It makes use of Bayes’ theorem to regulate preliminary beliefs based mostly on new info. This method combines what’s recognized earlier than with new information successfully. This method quantifies uncertainty and adjusts possibilities accordingly. On this manner, it constantly improves predictions and understanding as extra proof is gathered. It’s helpful in decision-making the place uncertainty must be managed successfully.

Instance: In scientific trials, Bayesian strategies estimate the effectiveness of recent remedies. They mix prior beliefs from previous research or with present information. This updates the likelihood of how properly the remedy works. Researchers can then make higher selections utilizing outdated and new info.

Predictive Modeling and Uncertainty Quantification

Predictive modeling and uncertainty quantification contain making predictions and understanding how assured we’re in these predictions. It makes use of strategies like Bayesian strategies to account for uncertainty and supply probabilistic forecasts. Bayesian modeling is efficient for predictions as a result of it manages uncertainty. It doesn’t simply predict outcomes but additionally signifies our confidence in these predictions. That is achieved via posterior distributions, which quantify uncertainty.

Instance: Bayesian regression predicts inventory costs by providing a spread of doable costs moderately than a single prediction. Merchants use this vary to keep away from threat and make funding selections.

Bayesian Neural Networks

Bayesian neural networks (BNNs) are neural networks that present probabilistic outputs. They provide predictions together with measures of uncertainty. As an alternative of fastened parameters, BNNs use likelihood distributions for weights and biases. This enables BNNs to seize and propagate uncertainty via the community. They’re helpful for duties requiring uncertainty measurement and decision-making. They’re utilized in classification and regression.

Instance: In fraud detection, Bayesian networks analyze relationships between variables like transaction historical past and person habits to identify uncommon patterns linked to fraud. They enhance the accuracy of fraud detection techniques as in comparison with conventional approaches.

Instruments and Libraries for Bayesian Evaluation

A number of instruments and libraries can be found to implement Bayesian strategies successfully. Let’s get to find out about some in style instruments.

PyMC4

It’s a library for probabilistic programming in Python. It helps with Bayesian modeling and inference. It builds on the strengths of its predecessor, PyMC3. It introduces vital enhancements via its integration with JAX. JAX presents automated differentiation and GPU acceleration. This makes Bayesian fashions sooner and extra scalable.

Stan

A probabilistic programming language applied in C++ and out there via varied interfaces (RStan, PyStan, CmdStan, and so on.). Stan excels in effectively performing HMC and NUTS sampling and is understood for its velocity and accuracy. It additionally consists of in depth diagnostics and instruments for mannequin checking.

TensorFlow Chance

It’s a library for probabilistic reasoning and statistical evaluation in TensorFlow. TFP offers a spread of distributions, bijectors, and MCMC algorithms. Its integration with TensorFlow ensures environment friendly execution on numerous {hardware}. It permits customers to seamlessly mix probabilistic fashions with deep studying architectures. This text helps in strong and data-driven decision-making.

Let’s have a look at an instance of Bayesian Statistics utilizing PyMC4. We’ll see tips on how to implement Bayesian linear regression.

import pymc as pm
import numpy as np

# Generate artificial information
np.random.seed(42)
X = np.linspace(0, 1, 100)
true_intercept = 1
true_slope = 2
y = true_intercept + true_slope * X + np.random.regular(scale=0.5, measurement=len(X))

# Outline the mannequin
with pm.Mannequin() as mannequin:
    # Priors for unknown mannequin parameters
    intercept = pm.Regular("intercept", mu=0, sigma=10)
    slope = pm.Regular("slope", mu=0, sigma=10)
    sigma = pm.HalfNormal("sigma", sigma=1)
    
    # Chance (sampling distribution) of observations
    mu = intercept + slope * X
    probability = pm.Regular("y", mu=mu, sigma=sigma, noticed=y)
    
    # Inference
    hint = pm.pattern(2000, return_inferencedata=True)

# Summarize the outcomes
print(pm.abstract(hint))

Now, let’s perceive the code above step-by-step.

• It units preliminary beliefs (priors) for the intercept, slope, and noise.
• It defines a probability operate based mostly on these priors and the noticed information.
• The code makes use of Markov Chain Monte Carlo (MCMC) sampling to generate samples from the posterior distribution.
• Lastly, it summarizes the outcomes to point out estimated parameter values and uncertainties.

Wrapping Up

Bayesian strategies mix prior beliefs with new proof for knowledgeable decision-making. They enhance predictive accuracy and handle uncertainty in a number of domains. Instruments like PyMC4, Stan, and TensorFlow Chance present strong help for Bayesian evaluation. These instruments help make probabilistic predictions from advanced information.
 
 

Jayita Gulati is a machine studying fanatic and technical author pushed by her ardour for constructing machine studying fashions. She holds a Grasp’s diploma in Laptop Science from the College of Liverpool.