Dijkstra Algorithm in Python

Introduction

Suppose you’re over a map of roads, and also you need to know easy methods to get from one metropolis to a different utilizing the fewest doable roads. When delivering merchandise by way of metropolis roads or trying to find the best route in a community or different programs, the shortest route is essential. Nevertheless, among the best algorithms utilized in fixing them is the Dijkstra’s Algorithm. Additionally initially thought by Edsger W. Dijkstra in 12 months 1956, this algorithm successfully finds all shortest paths in a weighted graph through which every arc comes with a non destructive weight. Right here on this tutorial, we are going to present you easy methods to implement Dijkstra’s Algorithm in steps and for sensible use in Python.

Studying Outcomes

• Perceive the ideas behind Dijkstra’s Algorithm.
• Have the ability to implement Dijkstra’s Algorithm in Python.
• Discover ways to deal with weighted graphs and calculate the shortest paths between nodes.
• Know easy methods to optimize and tweak the algorithm for efficiency in Python.
• Achieve hands-on expertise by fixing a real-world shortest path downside utilizing Python.

What’s Dijkstra’s Algorithm?

The algorithm is a grasping algorithm that helps establish the shortest path on a graph that begins with one node. Particularly, within the case of the non-negative weight of edges, the algorithm demonstrates a low complexity. A key concept is to have a pool of nodes for which there exists a finest identified distance from the supply and the growth to the set of nodes is finished by selecting a node with the least identified distance. This course of continues till and all nodes have been processed.

Right here’s a fundamental breakdown of the algorithm:

• Assign a tentative distance worth to each node: set it to 0 for the preliminary node and to infinity for all others.
• Set the preliminary node as present and mark all different nodes as unvisited.
• For the present node, examine all its unvisited neighbors and calculate their tentative distances by way of the present node. If this distance is lower than the beforehand recorded tentative distance, replace the space.
• As soon as achieved with the neighbors, mark the present node as visited. A visited node is not going to be checked once more.
• Choose the unvisited node with the smallest tentative distance as the brand new present node and repeat steps 3-4.
• Proceed the method till all nodes are visited or the shortest distance to the goal node is discovered.

Key Ideas Behind Dijkstra’s Algorithm

Earlier than diving into the implementation, it’s important to know some key ideas:

• Graph Illustration: The algorithm expects the graph to be achieved utilizing nodes and edges. Each edge comes with weight – the that means of which is the space or value estimated between two nodes.
• Precedence Queue: The bottom algorithm that Dijkstra’s Algorithm can make use of is the precedence queue that determines the subsequent node within the shortest distance.
• Grasping Strategy: The algorithm enlarges the shortest identified area by yielding the closest impartial node with respect to a centered node.

Methods to Implement Dijkstra Algorithm?

We are going to now implement the Dijkstra algorithm step-by-step utilizing Python. We’ll signify the graph as a dictionary the place keys are nodes and values are lists of tuples representing the adjoining nodes and their corresponding weights.

Step1: Initialize the Graph

We have to signify the graph we’re working with. We’ll use a dictionary the place the keys are the nodes, and the values are lists of tuples representing the adjoining nodes and their corresponding weights.

graph = {
    'A': [('B', 1), ('C', 4)],
    'B': [('A', 1), ('C', 2), ('D', 5)],
    'C': [('A', 4), ('B', 2), ('D', 1)],
    'D': [('B', 5), ('C', 1)]
}

This graph represents a community the place:

• Node A connects to B with weight 1 and to C with weight 4.
• Node B connects to A, C, and D, and so forth.

Step 2: Outline the Algorithm

Subsequent, we are going to outline the Dijkstra algorithm itself. This operate will take the graph and a beginning node as enter and return the shortest distances from the beginning node to each different node within the graph. We are going to use Python’s heapq to implement a precedence queue to at all times discover the node with the smallest identified distance first.

import heapq

def dijkstra(graph, begin):
    # Initialize distances from the beginning node to infinity for all nodes besides the beginning node
    distances = {node: float('infinity') for node in graph}
    distances[start] = 0
    # Precedence queue to retailer nodes for exploration
    pq = [(0, start)]  # (distance, node)

    whereas pq:
        current_distance, current_node = heapq.heappop(pq)

        # Skip this node if it has already been processed with a shorter distance
        if current_distance > distances[current_node]:
            proceed

        # Discover neighbors
        for neighbor, weight in graph[current_node]:
            distance = current_distance + weight

            # Solely contemplate this path if it is higher than the beforehand identified one
            if distance < distances[neighbor]:
                distances[neighbor] = distance
                heapq.heappush(pq, (distance, neighbor))

    return distances

Step 3: Run the Algorithm

With the algorithm outlined, we will now run it on our graph. Right here, we’ll specify a beginning node (on this case, ‘A’) and name the operate to seek out the shortest paths from ‘A’ to all different nodes.

start_node="A"
shortest_paths = dijkstra(graph, start_node)
print(f"Shortest paths from {start_node}: {shortest_paths}")

The output would present the shortest path from node A to all different nodes.

Step 4: Understanding the Output

After working the code, the output will show the shortest paths from the beginning node (A) to all different nodes within the graph.

If we run the code above, the output will likely be:

Shortest paths from A: {'A': 0, 'B': 1, 'C': 3, 'D': 4}

This consequence tells us that:

• The shortest path from A to B is 1.
• The shortest path from A to C is 3.
• The shortest path from A to D is 4.

Instance of Dijkstra’s Algorithm

Under we are going to see the instance of Dijkstra’s Algorithm intimately:

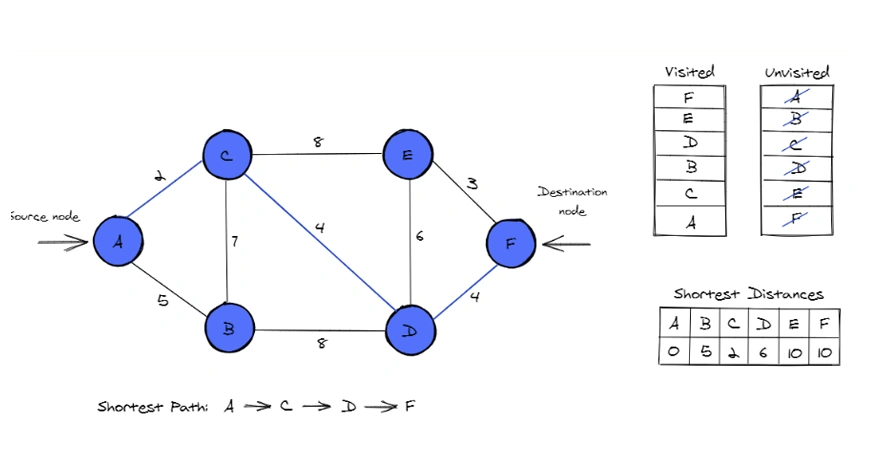
Rationalization of the Course of

• The algorithm begins on the supply node A and calculates the shortest path to all different nodes by evaluating the sting weights between linked nodes.
• Visited and unvisited nodes: Dijkstra’s Algorithm makes use of two units of nodes – visited and unvisited. Initially, solely the supply node (A) is marked as visited, and the remainder are thought-about unvisited. Because the algorithm progresses, it visits nodes so as of accelerating shortest distance.
• Shortest Distances: The shortest distances are regularly up to date because the algorithm evaluates all doable paths. Every node is assigned a distance worth, beginning with 0 for the supply node and infinity for the others. As higher paths are discovered, the distances are up to date.

Steps Concerned

• Ranging from node A, the algorithm checks its neighbors and calculates the tentative distances to them. The neighbors are B and C, with distances of seven and 5, respectively.
• The algorithm chooses node C (distance 5) as the subsequent node to go to because it has the smallest distance.
• From node C, the algorithm evaluates the neighboring nodes D and E, updating their distances.
• The shortest path to node D is discovered, so the algorithm strikes to node D.
• From node D, it evaluates the trail to the ultimate node, F.
• After visiting all related nodes, the shortest path to node F is set to be 10.

Closing Output

The shortest path from A to F is A → C → D → F, with a complete distance of 10.

Shortest Distances

The shortest distance to every node from the supply node A is:

• A → A: 0
• A → B: 7
• A → C: 5
• A → D: 6
• A → E: 10
• A → F: 10

The algorithm effectively calculated the shortest path utilizing the precept of visiting the closest unvisited node and updating distances primarily based on the sides connecting them.

Enhancements to Dijkstra’s Algorithm

Dijkstra’s Algorithm will be enhanced in numerous methods to enhance its efficiency, particularly for giant or particular purposes. Under are some key optimizations:

Early Stopping for Focused Searches

If what you need is solely the shortest path from the supply node to the vacation spot node then you’ll be able to make use of early stopping. After reaching the goal node it may be stopped as a result of then further nodes will be neglected and have much less play on this specific algorithm.

Bidirectional Dijkstra’s Algorithm

By working Dijkstra’s Algorithm from each the beginning and goal nodes concurrently, bidirectional Dijkstra reduces the search area. The 2 searches meet within the center, considerably rushing up the method in giant graphs.

Optimizing Graph Illustration

For sparse graphs, utilizing an adjacency checklist saves reminiscence and accelerates the algorithm. In dense graphs, an adjacency matrix will be extra environment friendly for edge lookups. Selecting the best graph illustration can have a major influence on efficiency.

Utilizing a Fibonacci Heap

A Fibonacci heap improves the time complexity of Dijkstra’s Algorithm from O((V + E) log V) to O(E + V log V) by making precedence queue operations sooner. Although extra advanced to implement, it’s useful for very giant graphs with many nodes and edges.

Reminiscence Effectivity in Sparse Graphs

For giant, sparse graphs, contemplate lazy loading elements of the graph or compressing the graph to scale back reminiscence utilization. That is helpful in purposes like highway networks or social graphs the place reminiscence can turn into a limiting issue.

Actual-World Purposes of Dijkstra’s Algorithm

Dijkstra’s Algorithm has quite a few purposes throughout numerous industries resulting from its effectivity in fixing shortest path issues. Under are some key real-world use circumstances:

GPS and Navigation Methods

Different GPS comparable to Google Map and Waze, additionally apply Dijkstra’s Algorithm to find out the shortest path between two locations. It assists customers to find one of the best routes relying on roads shared to help in real-time by offering site visitors patterns or congestion, highway blockage, or spillage. These programs are additional improved by function enhancements comparable to early stopping and bidirectional search to seek out the shortest doable hyperlink between two given factors.

Community Routing Protocols

Different protocols comparable to OSPF (Open Shortest Path First) in Laptop networking software Dijkstra’s algorithm for analyzing the very best path for knowledge packet to journey in a community. Knowledge is subsequently transmitted with a lot ease, therefore lowering congestion on the linked networks within the system and therefore making the general velocity of the system very environment friendly.

Telecommunications and Web Infrastructure

Many telecommunication firms apply Dijkstra’s Algorithm within the method through which the communication’s sign is laid to swimsuit the cables, routers and servers it’s going to cross by way of. This enables data to be relayed by way of the shortest and finest channels doable and cut back probabilities of delays and breaks of the channels.

AI and Robotics Pathfinding

In robotics and synthetic intelligence conferences, conventions, and purposes, Dijkstra’s Algorithm is employed in path-searching strategies that are environments with limitations for robotic or autonomous programs. Because it helps the robots transfer within the shortest distance whereas on the identical time avoiding object and different obstacles, the algorithm could be very important for purposes comparable to warehousing and automotive the place robotic autos at the moment are used.

Sport Growth

In all probability the preferred use of Dijkstra’s Algorithm is used within the improvement of video games for path discovering in video games. Characters as NPCs in video games have to maneuver by way of digital surroundings and paths are sometimes optimized and for this Dijkstra helps in giving shortest path amongst two factors and avoids hindrances throughout recreation play.

Widespread Pitfalls and Methods to Keep away from Them

There are some errors which might be typical for this algorithm and we must always watch out for them. Under are just a few, together with tips about easy methods to keep away from them:

Dealing with Adverse Edge Weights

Pitfall: The limitation to this kind of algorithm is that it doesn’t acknowledge destructive weights for edges, subsequently produces incorrect outcomes.

Resolution: In case your graph incorporates destructive weights then, it’s preferable to make use of algorithms comparable to Bellman-Ford to resolve it, in any other case, normalize all of the weights of the graph to be non-negative earlier than utilizing Dijkstra every case.

Inefficient Precedence Queue Administration

Pitfall: Utilizing an inefficient knowledge construction for the precedence queue (like a easy checklist) can drastically decelerate the algorithm, particularly for giant graphs.

Resolution: All the time implement the precedence queue utilizing a binary heap (e.g., Python’s heapq), and even higher, a Fibonacci heap for sooner decrease-key operations in giant graphs.

Reminiscence Overhead in Giant Graphs

Pitfall: Storing giant graphs totally in reminiscence, particularly dense graphs, can result in extreme reminiscence utilization, inflicting efficiency bottlenecks or crashes.

Resolution: Optimize your graph illustration primarily based on the kind of graph (sparse or dense). For sparse graphs, use an adjacency checklist; for dense graphs, an adjacency matrix could also be extra environment friendly. In very giant graphs, contemplate lazy loading or graph compression strategies.

Ignoring Early Stopping in Particular Searches

Pitfall: Persevering with the algorithm after the shortest path to the goal node has been discovered can waste computational sources.

Resolution: Implement early stopping by terminating the algorithm as quickly because the shortest path to the goal node is set. That is particularly vital for giant graphs or point-to-point searches.

Failing to Select the Proper Algorithm for the Job

Pitfall: Utilizing Dijkstra’s Algorithm in eventualities the place a distinct algorithm could be extra appropriate, comparable to graphs with destructive weights or circumstances requiring sooner heuristic-based options.

Resolution: Analyze your graph and the issue context. If destructive weights are current, go for the Bellman-Ford Algorithm. For giant graphs the place an approximate answer is appropriate, think about using A search* or Grasping algorithms.

Conclusion

Dijkstra’s Algorithm will be described as an efficient method in addressing shortest path issues in circumstances the place weights are non-negative. It’s relevant to totally different areas which embrace improvement of networks to video games. Following this tutorial, you at the moment are capable of carry out Dijkstra’s Algorithm in Python by creating and modifying the given code. Altogether this implementation is sweet to have if one offers with routing issues or would love merely to find out about graph algorithms.

Regularly Requested Questions