Introduction
Computing sq. root is a crucial idea in arithmetic and inside this programming language one is ready to embark on this primary computation in a quite simple and environment friendly method. Whether or not you’re concerned in an experiment, simulations, information evaluation or utilizing machine studying, calculating sq. roots in Python is essential. On this information, you’ll study varied methods of approximating sq. root in Python; whether or not it’s by use of inbuilt capabilities or by utilizing different developed python libraries that are environment friendly in fixing arithmetic computation.
Studying Outcomes
- Perceive what a sq. root is and its significance in programming.
- Learn to compute sq. roots utilizing Python’s built-in
mathmodule. - Uncover alternative routes to seek out sq. roots utilizing exterior libraries like
numpy. - Be capable of deal with edge instances resembling destructive numbers.
- Implement sq. root calculations in real-world examples.
What’s a Sq. Root?
A sq. root of a quantity is a worth that, when multiplied by itself, leads to the unique quantity. Mathematically, if y is the sq. root of x, then:
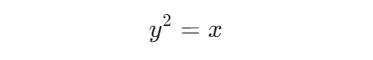
This implies 𝑦 × 𝑦 = 𝑥. For instance, the sq. root of 9 is 3 as a result of 3 × 3 = 9.
Notation:
The sq. root of a quantity xxx is usually denoted as:
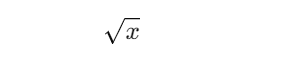
Why It’s Essential to Perceive Sq. Roots
Sq. roots are important throughout arithmetic, sciences, and technical professions as a result of they floor understanding of those operations. Whether or not you might be simply doing addition and subtraction, or fixing equations that contain tough algorithms, the understanding of how sq. roots work can allow you resolve many issues successfully. Under are a number of key the explanation why understanding sq. roots is necessary:
- Basis for Algebra: Sq. roots are important for fixing quadratic equations and understanding powers and exponents.
- Geometry and Distance: Sq. roots assist calculate distances, areas, and diagonals, particularly in geometry and structure.
- Physics and Engineering: Key formulation in physics and engineering, like velocity and stress evaluation, contain sq. roots.
- Monetary Calculations: Utilized in threat evaluation, normal deviation, and progress fashions in finance and economics.
- Knowledge Science & Machine Studying: Sq. roots are important in optimization algorithms, error measurements, and statistical capabilities.
- Constructing Drawback-Fixing Abilities: Enhances mathematical reasoning and logic for tackling extra advanced issues.
Strategies to Compute Sq. Roots in Python
Python being an open supply language, there are numerous methods to reach on the sq. root of a quantity relying on the conditions at hand. Under are the most typical strategies, together with detailed descriptions:
Utilizing the math.sqrt() Operate
The easy and normal technique for locating the sq. root of a floating quantity in Python makes use of the mathematics.sqrt() perform from the inbuilt math library.
Instance:
import math
print(math.sqrt(25)) # Output: 5.0
print(math.sqrt(2)) # Output: 1.4142135623730951The math.sqrt() perform solely works with non-negative numbers and returns a float. If a destructive quantity is handed, it raises a ValueError.
Utilizing the cmath.sqrt() Operate for Advanced Numbers
For instances the place it is advisable compute the sq. root of destructive numbers, the cmath.sqrt() perform from the cmath (advanced math) module is used. This technique returns a fancy quantity in consequence.
This technique permits the computation of sq. roots of each optimistic and destructive numbers. It returns a fancy quantity (within the type of a + bj) even when the enter is destructive.
Instance:
import cmath
print(cmath.sqrt(-16)) # Output: 4j
print(cmath.sqrt(25)) # Output: (5+0j)It’s used when working with advanced numbers or when destructive sq. roots must be calculated.
Utilizing the Exponentiation Operator **
In Python, the exponentiation operator (**) can be utilized to calculate sq. roots by elevating a quantity to the facility of 1/2 (0.5).
This technique works for each integers and floats. If the quantity is optimistic, it returns a float. If the quantity is destructive, it raises a ValueError, as this technique doesn’t deal with advanced numbers.
Instance:
print(16 ** 0.5) # Output: 4.0
print(2 ** 0.5) # Output: 1.4142135623730951A fast and versatile technique that doesn’t require importing any modules, appropriate for easy calculations.
Utilizing Newton’s Methodology (Iterative Approximation)
Newton and its different identify the Babylonian technique is a straightforward algorithm to estimate the sq. root of a given amount. This technique is as follows and isn’t as simple because the built-in capabilities: Nevertheless, by doing this, one will get to grasp how sq. roots are computed within the background.
This one merely begins with some guess, often center worth, after which iteratively refines this guess till the specified precision is attained.
Instance:
def newtons_sqrt(n, precision=0.00001):
guess = n / 2.0
whereas abs(guess * guess - n) > precision:
guess = (guess + n / guess) / 2
return guess
print(newtons_sqrt(16)) # Output: roughly 4.0
print(newtons_sqrt(2)) # Output: roughly 1.41421356237Helpful for customized precision necessities or academic functions to exhibit the approximation of sq. roots.
Utilizing the pow() Operate
Python additionally has a built-in pow() perform, which can be utilized to calculate the sq. root by elevating the quantity to the facility of 0.5.
Instance:
num = 25
end result = pow(num, 0.5)
print(f'The sq. root of {num} is {end result}')
#Output: The sq. root of 25 is 5.0Utilizing numpy.sqrt() for Arrays
In case you are doing operations with arrays or matrices, within the numpy library there’s the numpy.sqrt() perform which is optimized for such calculations as acquiring sq. root of each factor within the array.
One of many advantages of utilizing this strategy is that to seek out sq. root of matching factor you don’t recompute the entire trigonometric chain, so is appropriate for large information units.
Instance:
import numpy as np
arr = np.array([4, 9, 16, 25])
print(np.sqrt(arr)) # Output: [2. 3. 4. 5.]Perfect for scientific computing, information evaluation, and machine studying duties the place operations on giant arrays or matrices are frequent.
Comparability of Strategies
Under is the desk of evaluating the strategies of python sq. root strategies:
| Methodology | Handles Adverse Numbers | Handles Advanced Numbers | Perfect for Arrays | Customizable Precision |
|---|---|---|---|---|
math.sqrt() |
No | No | No | No |
cmath.sqrt() |
Sure | Sure | No | No |
Exponentiation (**) |
No | No | No | No |
| Newton’s Methodology | No (with out advanced dealing with) | No (with out advanced dealing with) | No | Sure (with customized implementation) |
numpy.sqrt() |
No | Sure | Sure | No |
Actual-World Use Instances for Sq. Roots
- In Knowledge Science: Clarify how sq. roots are used to calculate normal deviation, variance, and root imply sq. errors in machine studying fashions.
import numpy as np
information = [2, 4, 4, 4, 5, 5, 7, 9]
standard_deviation = np.std(information)
print(f"Customary Deviation: {standard_deviation}")- In Graphics & Animation: Sq. roots are generally utilized in computing distances between factors (Euclidean distance) in 2D or 3D areas.
point1 = (1, 2)
point2 = (4, 6)
distance = math.sqrt((point2[0] - point1[0])**2 + (point2[1] - point1[1])**2)
print(f"Distance: {distance}") # Output: 5.0- Visualization: We are able to use python sq. root for visualizing the info.
import matplotlib.pyplot as plt
import numpy as np
x = np.linspace(0, 10, 100)
y = np.sqrt(x)
plt.plot(x, y)
plt.title("Sq. Root Operate")
plt.xlabel("x")
plt.ylabel("sqrt(x)")
plt.present()Efficiency Concerns and Optimization
Add a bit evaluating the computational effectivity of various sq. root strategies, particularly when working with giant datasets or real-time techniques.
Instance:
import timeit
print(timeit.timeit("math.sqrt(144)", setup="import math"))
print(timeit.timeit("144 ** 0.5"))This may spotlight the professionals and cons of utilizing one technique over one other, particularly when it comes to execution velocity and reminiscence consumption.
Dealing with Edge Instances
Dealing with edge instances is essential when working with sq. root calculations in Python to make sure robustness and accuracy. This part will discover the best way to handle particular instances like destructive numbers and invalid inputs successfully.
- Error Dealing with: Focus on the best way to deal with exceptions when calculating sq. roots, resembling utilizing
try-exceptblocks to handleValueErrorfor destructive numbers inmath.sqrt().
strive:
end result = math.sqrt(-25)
besides ValueError:
print("Can not compute the sq. root of a destructive quantity utilizing math.sqrt()")- Advanced Roots: Present extra detailed examples for dealing with advanced roots utilizing
cmath.sqrt()and clarify when such instances happen, e.g., in sign processing or electrical engineering.
Conclusion
Python provides a number of selections with regards to utilizing for sq. roots; the essential sort is math.sqrt() whereas the extra developed sort is numpy.sqrt() for arrays. Thus, you’ll be able to choose the required technique to make use of for a selected case. Moreover, information of the best way to use cmath to unravel particular instances like using destructive numbers will assist to make your code considerable.
Often Requested Questions
A. The best means is to make use of the math.sqrt() perform, which is easy and efficient for many instances.
A. But there’s a cmath.sqrt() perform which takes advanced quantity and turns into imaginary for ratio lower than zero.
A. Sure, by utilizing the numpy.sqrt() perform, you’ll be able to calculate the sq. root for every factor in an array or listing.
A. Passing a destructive quantity to math.sqrt() will increase a ValueError as a result of sq. roots of destructive numbers usually are not actual.
pow(x, 0.5) the identical as math.sqrt(x)?
A. Sure, pow(x, 0.5) is mathematically equal to math.sqrt(x), and each return the identical end result for non-negative numbers.