What’s Adaptive Gradient(Adagrad) Optimizer?

Think about you’re planting a backyard with a wide range of crops, every requiring a distinct quantity of water. When you used the identical quantity of water on all of them every single day, some crops would thrive, whereas others would possibly get overwatered or dry out. In machine studying, an analogous problem exists with gradient descent, the place utilizing the identical studying charge for all parameters can decelerate studying or result in poor efficiency. That is the place Adagrad is available in. It adjusts the step dimension for every parameter based mostly on how a lot it has modified throughout coaching, serving to the mannequin adapt to the distinctive “wants” of every characteristic, particularly once they range in scale.

What’s Adagrad(Adaptive Gradient)?

Adagrad (Adaptive Gradient) is an optimization algorithm extensively utilized in machine studying, significantly for coaching deep neural networks. It dynamically adjusts the educational charge for every parameter based mostly on its previous gradients. This adaptability enhances coaching effectivity, particularly in eventualities involving sparse information or parameters that converge at totally different charges.

By assigning larger studying charges to much less frequent options and decrease charges to extra frequent ones, Adagrad excels in dealing with sparse information. Furthermore, it eliminates the necessity for guide studying charge changes, simplifying the coaching course of.

Working of Adagrad Algorithm?

Step 1: Initialize Parameters

Step one in Adagrad is to initialize the mandatory elements earlier than beginning the optimization course of. The parameters being optimized, corresponding to weights in a neural community, are given preliminary values, usually random or zero, relying on the appliance. Alongside the parameters, a small fixed epsilon ϵ is about, to keep away from division by zero errors in later computations. Lastly, the preliminary studying charge is chosen to regulate how massive the parameter updates are at every step. The training charge is often chosen based mostly on experimentation or prior information about the issue. These preliminary settings are essential as a result of they affect the behaviour of the optimizer and its skill to converge to an answer.

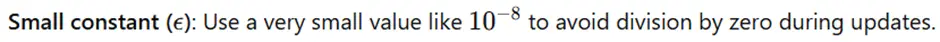
Step 2: Compute the Gradient

At every time step t, the gradient of the loss operate with respect to every parameter is calculated. This gradient signifies the course and magnitude of the adjustments wanted to cut back the loss. The gradient gives the “slope” of the loss operate, displaying how the parameters needs to be adjusted to reduce the error. This computation is repeated for all parameters and is crucial as a result of it guides the optimizer in updating the parameters successfully. The accuracy and stability of those gradients rely on the properties of the loss operate and the information getting used.

g_t​ = ∇f(θ_t​)

• f(θ_t​): Loss Perform
• g_t​: present gradient

Step 3: Accumulate the Squared Gradients

As a substitute of making use of the gradient on to replace the parameters, Adagrad introduces an accumulation step the place the squared gradients are summed over time. For every parameter ‘i’, this accrued squared gradient​ is computed as:

G_t​=G_t−1​+g_t²

• G_t−1​: Gathered squared gradients from earlier steps.
• g_t^2​: Sq. of the present gradient (element-wise if vectorized).

This step ensures that the optimizer retains monitor of how a lot every parameter has been up to date traditionally. Parameters with massive accrued gradients are successfully “penalized” in subsequent updates, whereas these with smaller accrued gradients retain larger studying charges. This mechanism permits Adagrad to dynamically alter the educational charge for every parameter, making it significantly helpful in circumstances the place gradients differ considerably throughout parameters, corresponding to in sparse information eventualities.

Step 4: Replace the Parameters

As soon as the accrued gradient is computed, the parameters are up to date utilizing Adagrad’s replace rule:

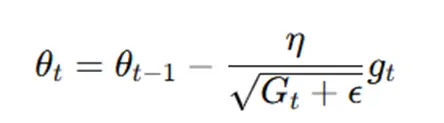
The denominator adjusts the educational charge for every parameter based mostly on its accrued gradient historical past. Parameters with massive accrued gradients have smaller updates as a result of bigger denominator, which prevents overshooting and promotes stability. Conversely, parameters with small accrued gradients have bigger updates, guaranteeing they don’t seem to be uncared for throughout coaching. This adaptive adjustment of studying charges permits Adagrad to deal with various parameter sensitivities successfully.

Additionally learn: Gradient Descent Algorithm: How Does it Work in Machine Studying?

How Adagrad Adapts the Studying Price?

Parameters with frequent updates :

Massive accrued gradients trigger the time period to shrink.

This reduces the educational charge for these parameters, slowing down their updates to forestall instability.

Parameters with rare updates:

Small accrued gradients maintain bigger.

This ensures bigger updates for these parameters, enabling efficient studying.

Why Adagrad’s Adjustment Issues?

Adagrad’s dynamic studying charge adjustment makes it significantly well-suited for issues the place some parameters require frequent updates whereas others are up to date much less usually. For instance, in pure language processing, phrases that seem ceaselessly within the information may have massive accrued gradients, decreasing their studying charges and stabilizing their updates. In distinction, uncommon phrases will retain larger studying charges, guaranteeing they obtain sufficient updates. Nevertheless, the buildup of squared gradients may cause the educational charges to decay an excessive amount of over time, slowing convergence in lengthy coaching periods. Regardless of this disadvantage, Adagrad is a strong and intuitive optimization algorithm for eventualities the place per-parameter studying charge adaptation is helpful.

Additionally learn: Full Information to Gradient-Primarily based Optimizers in Deep Studying

Implementation for Higher Understanding

1. Importing Essential Libraries

import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler

2. Outline the Gradient Descent Linear Regression Class

class GradientDescentLinearRegression:
    def __init__(self, learning_rate=1, max_iterations=10000, eps=1e-6):
        # Initialize hyperparameters
        self.learning_rate = learning_rate
        self.max_iterations = max_iterations
        self.eps = eps

The __init__ methodology initializes the category by setting key hyperparameters for gradient descent optimization: learning_rate, which controls the step dimension for weight updates; max_iterations, the utmost variety of iterations to forestall infinite loops; and eps, a small threshold for stopping the optimization when weight adjustments are negligible, signaling convergence. These parameters make sure the coaching course of is each environment friendly and exact, with flexibility for personalisation based mostly on the dataset and necessities. As an example, customers can modify these values to steadiness velocity and accuracy or depend on the default settings for normal functions.

3. Outline the Predict Technique

def predict(self, X):
        return np.dot(X, self.w.T)
    

This methodology calculates predictions by computing the dot product of the enter options (X) and the burden vector (w). It represents the core performance of linear regression, the place the anticipated values are a linear mixture of the enter options.

4. Outline the Price Strategies

def price(self, X, y):
        y_pred = self.predict(X)
        loss = (y - y_pred) ** 2
        return np.imply(loss)

The fee methodology calculates the Imply Squared Error (MSE) loss, which measures the distinction between precise goal values (y) and predicted values (y_pred). This operate guides the optimization course of by quantifying the mannequin’s efficiency.

5. Outline the Grad Technique

def grad(self, X, y):
        y_pred = self.predict(X)
        d_intercept = -2 * sum(y - y_pred)                  
        d_x = -2 * sum(X[:, 1:] * (y - y_pred).reshape(-1, 1))  
        g = np.append(np.array(d_intercept), d_x)          
        return g / X.form[0]

This methodology computes the gradient of the associated fee operate in regards to the mannequin’s weights. The gradient signifies the course wherein the weights needs to be adjusted to reduce the associated fee. It individually computes the gradients for the intercept and have weights.

6. Outline the Adagrad Technique

def adagrad(self, g):
        self.G += g**2  
        step = self.learning_rate / (np.sqrt(self.G + self.eps)) * g
        return step

The Adagrad methodology implements the AdaGrad optimization approach, which adjusts the educational charge for every weight dynamically based mostly on the accrued gradient squared (G). This method is especially efficient for sparse information or when coping with weights up to date at various charges.

7. Outline the Match Technique

def match(self, X, y, methodology="adagrad", verbose=True):
        # Initialize weights and AdaGrad cache if wanted
        self.w = np.zeros(X.form[1])  # Initialize weights
        if methodology == "adagrad":
            self.G = np.zeros(X.form[1])  # Initialize AdaGrad cache
        w_hist = [self.w]  # Historical past of weights
        cost_hist = [self.cost(X, y)]  # Historical past of price operate values
        for iter in vary(self.max_iterations):
            g = self.grad(X, y)  # Compute the gradient
            if methodology == "customary":
                step = self.learning_rate * g  # Customary gradient descent step
            elif methodology == "adagrad":
                step = self.adagrad(g)  # AdaGrad step
            else:
                elevate ValueError("Technique not supported.")
            self.w = self.w - step  # Replace weights
            w_hist.append(self.w)  # Save weight historical past
            J = self.price(X, y)  # Compute price
            cost_hist.append(J)  # Save price historical past
            if verbose:
                print(f"Iter: {iter}, Gradient: {g}, Weights: {self.w}, Price: {J}")
            # Cease if weight updates are smaller than the edge
            if np.linalg.norm(w_hist[-1] - w_hist[-2]) < self.eps:
                break
        # Retailer historical past and optimization methodology used
        self.iterations = iter + 1
        self.w_hist = w_hist
        self.cost_hist = cost_hist
        self.methodology = methodology
        return self   

The match methodology trains the linear regression mannequin utilizing gradient descent. It initializes the burden vector (w) and accumulates gradient info if utilizing AdaGrad. In every iteration, it computes the gradient, updates the weights, and calculates the present price. If the burden adjustments change into too small (lower than eps), the coaching halts early. Verbose output optionally gives detailed logs of the optimization course of.

Right here’s the complete code:

# Import mandatory libraries
import numpy as np
from sklearn.datasets import fetch_california_housing
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
# Outline the customized Gradient Descent Linear Regression class
class GradientDescentLinearRegression:
    def __init__(self, learning_rate=1, max_iterations=10000, eps=1e-6):
        # Initialize hyperparameters
        self.learning_rate = learning_rate
        self.max_iterations = max_iterations
        self.eps = eps
    def predict(self, X):
        return np.dot(X, self.w.T)  # Linear regression prediction: X*w^T
    def price(self, X, y):
        y_pred = self.predict(X)
        loss = (y - y_pred) ** 2
        return np.imply(loss)
    def grad(self, X, y):
        y_pred = self.predict(X)
        d_intercept = -2 * sum(y - y_pred)                  
        d_x = -2 * sum(X[:, 1:] * (y - y_pred).reshape(-1, 1))  
        g = np.append(np.array(d_intercept), d_x)          
        return g / X.form[0]                              
    def adagrad(self, g):
        self.G += g**2  
        step = self.learning_rate / (np.sqrt(self.G + self.eps)) * g
        return step
    def match(self, X, y, methodology="adagrad", verbose=True):
        # Initialize weights and AdaGrad cache if wanted
        self.w = np.zeros(X.form[1])  # Initialize weights
        if methodology == "adagrad":
            self.G = np.zeros(X.form[1])  # Initialize AdaGrad cache
        w_hist = [self.w]  # Historical past of weights
        cost_hist = [self.cost(X, y)]  # Historical past of price operate values
        for iter in vary(self.max_iterations):
            g = self.grad(X, y)  # Compute the gradient
            if methodology == "customary":
                step = self.learning_rate * g  # Customary gradient descent step
            elif methodology == "adagrad":
                step = self.adagrad(g)  # AdaGrad step
            else:
                elevate ValueError("Technique not supported.")
            self.w = self.w - step  # Replace weights
            w_hist.append(self.w)  # Save weight historical past
            J = self.price(X, y)  # Compute price
            cost_hist.append(J)  # Save price historical past
            if verbose:
                print(f"Iter: {iter}, Gradient: {g}, Weights: {self.w}, Price: {J}")
            # Cease if weight updates are smaller than the edge
            if np.linalg.norm(w_hist[-1] - w_hist[-2]) < self.eps:
                break
        # Retailer historical past and optimization methodology used
        self.iterations = iter + 1
        self.w_hist = w_hist
        self.cost_hist = cost_hist
        self.methodology = methodology
        return self
# Load the California housing dataset
information = fetch_california_housing()
X, y = information.information, information.goal
# Cut up the dataset into coaching and testing units
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# Standardize the characteristic information
scaler = StandardScaler()
X_train = scaler.fit_transform(X_train)
X_test = scaler.remodel(X_test)
# Prepare and consider the mannequin utilizing customary gradient descent
mannequin = GradientDescentLinearRegression(learning_rate=0.1, max_iterations=1000, eps=1e-6)
mannequin.match(X_train, y_train, methodology="customary", verbose=False)
y_pred = mannequin.predict(X_test)  # Predict take a look at information
mse = np.imply((y_test - y_pred) ** 2)  # Compute MSE
print("Last Weights (Customary):", mannequin.w)
print("Imply Squared Error (Customary GD):", mse)
# Prepare and consider the mannequin utilizing AdaGrad
mannequin = GradientDescentLinearRegression(learning_rate=0.1, max_iterations=1000, eps=1e-6)
mannequin.match(X_train, y_train, methodology="adagrad", verbose=False)
y_pred = mannequin.predict(X_test)  # Predict take a look at information
mse = np.imply((y_test - y_pred) ** 2)  # Compute MSE
print("Last Weights (AdaGrad):", mannequin.w)
print("Imply Squared Error (AdaGrad):", mse)

Additionally learn: A Complete Information on Optimizers in Deep Studying

Functions of Adagrad Optimizer

Listed below are the purposes of Adagrad Optimizer:

1. Pure Language Processing (NLP): Adagrad is extensively used for duties like sentiment evaluation, textual content classification, language modeling, and machine translation. Its adaptive studying charges are significantly efficient in optimizing sparse embeddings, that are frequent in NLP duties​.
2. Recommender Techniques: The optimizer is utilized to personalize suggestions by dynamically adjusting studying charges. This functionality helps fashions deal with sparse datasets, that are typical in advice eventualities​.
3. Time Collection Evaluation: It’s used for forecasting duties like inventory value predictions, the place information patterns might be non-uniform and want adaptive studying charge changes​.
4. Picture Recognition: Whereas not as frequent as different optimizers like Adam, Adagrad has been utilized in laptop imaginative and prescient duties for effectively coaching fashions the place sure options require larger studying charges​.
5. Speech and Audio Processing: Just like NLP, Adagrad can optimize fashions for duties like speech recognition and audio classification, particularly when dealing with sparse characteristic representations​

Limitations of Adagrad

Listed below are the constraints of Adagrad:

1. Aggressive Studying Price Decay: Adagrad accumulates the squared gradients over all iterations. This accumulation grows constantly, resulting in a drastic discount within the studying charge.This aggressive decay may cause the algorithm to cease studying prematurely, particularly in later phases of coaching.
2. Poor Efficiency on Non-Convex Issues: For complicated non-convex optimization issues, Adagrad’s lowering studying charge can hinder its skill to flee from saddle factors or native minima, slowing convergence.
3. Computational Overhead: Adagrad requires sustaining a per-parameter studying charge and accumulative squared gradients. This could result in elevated reminiscence consumption and computational overhead, particularly for large-scale fashions.

Conclusion

AdaGrad is without doubt one of the variants of optimization algorithms which have made large contributions towards advancing the event of machine studying. It creates adaptive studying charges particular to the wants of each sparse data-compatible parameter, adjusts step sizes, dynamically adjustments, and learns from it, which explains why it seems to be helpful in domains like pure language processing, recommender programs, and time-series evaluation.

Nevertheless, all of those strengths got here at a terrific price: sharp studying charge decay, poor optimization on nonconvex issues, and excessive computational overhead. This produced successors: AdaDelta and RMSProp, which averted the weaknesses of AdaGrad whereas conserving not less than a number of the fundamental strengths.

Regardless of all these limitations, AdaGrad intuitively and successfully is an effective selection for issues that both have sparse information or options with various sensitivities; therefore it’s a cornerstone within the evolution of adaptive optimization strategies. Its simplicity and effectiveness continued to make it foundational for learners and practitioners within the subject of machine studying.

If you’re in search of an AI/ML course on-line, then discover: Licensed AI & ML BlackBelt PlusProgram

Incessantly Requested Questions